Memahami Macam – Macam Pola Bilangan Dalam Matematika
Macam – macam pola bilangan | Pola bilangan merupakan sub bab dari materi barisan bilangan atau bab yang perlu di fahami terlebih dahulu sebelum melanjut pada materi barisan aritmatika dan barisan geometri .Pola bilangan juga merupakan materi yang tidak kalah penting untuk dipelajari .
Pola bilangan sendiri memiliki arti suatu susunan bilangan yang memiliki bentuk teratur atau suatu bilangan yang tersusun dari beberapa bilangan lain yang membentuk suatu pola . Dan pola bilanga juga memiliki banyak jenisnya atau macamnya . Pada kesempatan kali ini , kita akan mempelajarinya bersama .
Macam – macam Pola Bilangan
Macam – macam pola bilngan meliputi beberapa jenis berikut ini :
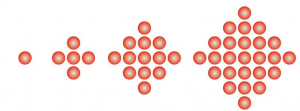
- Pola Bilangan Ganjil
Poal bilangan ganjil yaitu pola bilangan yang terbentuk dari bilangan – bilangan ganjil . Sedangkan pengertian dari bilangan ganjil sendiri memiliki arti suatu bilangan asli yang tidak habis dibagi dua ataupun kelipatannya .
- pola bilangan ganjil adalah : 1 , 3 , 5 , 7 , 9 , . . . .
- Gambar Pola bilangan ganjil :
- Rumus Pola Bilangan ganjil
1 , 3 , 5 , 7 , . . . , n , maka rumus pola bilangan ganjil ke n adalah :
Un = 2n – 1
Contoh :
1 , 3 , 5 , 7 , . . . , ke 10
Berapakah pola bilangan ganjil ke 10 ?
Jawab :
Un = 2n – 1
U10 = 2 . 10 – 1
= 20 – 1 = 19
2. Pola Bilangan Genap
pola bilangan genap yaitu pola bilangan yang terbentuk dari bilangan – bilangan genap . Bilangan genap yaitu bilangan asli yaitu bilangan asli yang habis dibagi dua atau kelipatannya .
- Pola bilangan genap adalah : 2 , 4 , 6 , 8 , . . .
- Gambar pola bilangan genap :
- Rumus Pola bilangan genap
2 , 4 , 6 , 8 , . . . . , n maka rumus pola bilangan genap ke n adalah :
Un = 2n
Contoh :
2 , 4 , 6 , 8 , . . . ke 10 .berapakah pola bilangan genap ke 10 ?
jawab :
Un = 2n
U10 = 2 x 10
= 20
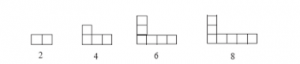
3. Pola bilangan Persegi
Pola bilangan persegi , yaitu suatu barisan bilangan yang membentuk suatu pola persegi .
- Pola bilangan persegi adalah 1 , 4 , 9 , 16 , 25 , . . .
- Gambar Pola bilangan persegi :
- Rumus Pola bilangan persegi
1 , 4 , 9 , 16 , 25 , 36 , . . . , n maka rumus untuk mencari pola bilangan persegi ke n adalah :
Un = n2
Contoh :
Dari suatu barisan bilangan 1 , 2 , 9 , 16 , 25 , 36 , . . . ,ke 10 . Berapakah pola bilangan ke 10 dalam pola bilangan persegi ?
Jawab :
Un = n2
U10 = 102 = 100
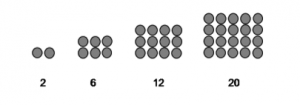
4. Pola Bilangan Persegi Panjang
Pola bilangan persegi panjang yaitu suatu barisan bilangan yang membentuk pola persegi panjang .
- Pola persegi panjang adalah 2 , 6 , 12 , 20 , 30 , . . .
- Gambar Pola Bilangan persegi panjang :
- Rumus pola bilangan persegi panjang
2 , 6 , 12 , 20 , 30 , . . . n , maka Rumus Pola bilangan Persegi panjang ke n adalah :
Un = n . n + 1
Contoh :
Dari suatu barisan bilangan 2 , 6 , 12 , 20 , 30 , . . . , ke 10 . Berapakah pola bilangan persegi ke 10 ?
Jawab :
Un = n . n+ 1
U10 = 10 . 10 + 1
= 10 . 11
= 110
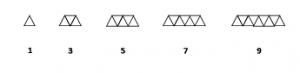
5. Pola Bilangan Segitiga
Pola bilangan segitiga yaitu suatu barisan bilangan yang membentuk sebuah pola bilangan segitiga .
- Pola bilangan segitiga adalah : 1 , 3 , 6 , 10 , 15 , . . .
- Gambar Pola bilangan segitiga :
- Rumus Pola Bilangan Segitiga :
1 , 3 , 6 , 10 , 15 , 21 , 28 , 36 , . . . , ke n . Maka rumus pola bilangan segitiga ke n adalah :
Un = 1 / 2 n ( n + 1 )
Contoh Soal :
Dari suatu barisan bilangan 1 , 3 , 6 , 10 , 15 , 21 , 28 , 36 , . . . , ke 10 . Berapakah pola bilangan segitiga ke 10 ?
Jawab :
Un = 1/2 n ( n + 1 )
U 10 = 1/2 .10 ( 10 + 1 )
= 5 ( 11 ) = 55
6. Pola Bilangan FIBONACCI
Pola bilangan fibonacci yaitu suatu bilangan yang setiap sukunya merupakan jumlah dari dua suku di depanya .
- Pola bilangan fibonacci :
1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 56 , . . .
2 , 2 , 4 , 6 , 10 , 16 , 26 , 42 , . . ..
Demikian penjelasan mengenai pola bilangan dalam ilmu matematika . Pada dasarnya , pola bilangan merupakan suatu bentuk barisan bilangan . Apabila kita dalam memperhatikanya tidak terlalu cermat, maka pola yang satu dengan pola bilangan yang lain tidak ada bedanya . Namun , pola bilangan memiliki fungsi yang sangat besar yaitu supaya lebih mudah dalam mengerjakan barisan aritmatika dan geometri . Semoga bermanfaat . . .
Sifat Bilangan Berpangkat Beserta Pengertiannya Dalam Matematika
Sifat Bilangan Berpangkat | Bilangan berpangkat merupakan salah satu cabang ilmu matematis yang dipelajari sejak kita duduk di bangku Sekolah Dasar . Dan merupakan bentuk kelanjutan dari operasi hitung yang terdiri dari penjumlahan , pengurangan , pembagian dan perkalian .
Sebelum kita mempelajari bilangan berpangkat lebih dalam , maka kita harus mengetahui terlebih dahulu pengertian dari bilangan berpangkat itu sendiri , baru kita mempelajari jenis dan sifat – sifat dari bilangan berpangkat .
Pengertian Dan sifat Bilangan Berpangkat
A. Pengertian bilangan berpangkat
Bilangan berpangkat , yaitu merupakan bilangan penyederhana dari sebuah bilangan yang di kalikan , atau untuk lebih memahaminya perhatikan penjelasan di bawah ini :
an = a x a x a x a x . . . .x n ( Sebanyak n )
Keterangan :
an = bilangan berpangkat
a = bilangan pokok
n = pangkat
B. Jenis – Jenis Bilangan Berpangkat
Bilangan berpangkat , terdiri dari beberapa jenis yaitu :
- Bilangan berpangkat bulat positif
yaitu merupakan penyederhanaan dari seatu perkalian bilangan bulat yang memiliki faktor yang sama .
Apabila dirumuskan adalah :
an = a x a x a x a x . . . .x n ( Sebanyak n )
Ket:
a = bilangan dasar ( bilangan pokok )
n = pangkat ( eksponen )
Contoh :
25 = 2 x 2 x 2 x 2 x 2 = 32
72 = 7 x 7 = 49
2. Bilangan Berpangkat bulat negatif
Yaitu merupakan bilangan yang pangkatnya merupakan bilangan negatif .
Apabila dirumuskan :
Contoh :
10-2 = 1 / 102
3. Bilangan Berpangkat Nol
Yaitu merupakan bilangan berpangkat yang pangkatnya nol . Dan semua bilangan yang di pangkatkan nol hasilnya 1.
Apabila dirumuskan :
a0 = 1
C. Sifat – sifat Bilangan Berpangkat
Untuk dapat megerjakan permasalahan – permasalahan di dalam soal bilangan berpangkat , kita harus mengetahui sifat – sifat bilangan berpangkat supaya kita dalam mengerjakannya kita memiliki tata aturan dasar atau sebagai pacuan dalam mengerjakannya dan supaya mempermudah dalam mengerjakannya .
Sifat – sifat bilangan berpangkat adalah sebagai berikut :
- Perkalian Bilangan Berpangkat
Dalam perkalian bilangan berpangkat , maka berlaku sifat seperti di bawah ini :
Contoh :
- 22 x 26 = 2 2+6 = 28
- 32 x 32 = 2 2+2 = 24
2. Pembagian Bilangan Berpangkat
Dalam pembagian bilangan berpangkat berlaku rumus :
Contoh :
- 36 : 32 = 2 6-2 = 24
- 66 : 63 = 66-3 = 63
3. Sifat Pemangkatan Bilangan Berpangkat
Apabila ada suatu bilangan berpagkat yang di pangkatkan lagi ,maka berlaku rumus :
(am)n = a m x n
Contoh :
( 23 ) 2 = 2 3 x 2 = 26
4. Sifat Perpangkatan Suatu Perkalian atau pembagian
- Apabila ada dua bilangan bulat yang dikalikan dan di pangkatkan maka berlaku rumus :
( a x b ) n = an x bn
- Apabila ada dua bilangan bulat yang di bagi dan di pangkatkan maka berlaku rumus :
( a : b ) n = an : bn
Contoh Soal
- Sederhanakan bentuk bilangan berpangkat berikut :
a.
b.
Penyelesaian :
a.
< = >( P6 / q -9 ) ( 4q2 /p6 )
< = >( P6 : 1/ q 9 ) (4q2 . p-6 )
< = > (P6 . q 9 ) (4q2 . p-6 )
< = > 4. P6 + (-6) . q 9+2
<= > 4. P0 . q 11
< = > 4.1. q 11
< = > 4 q 11
b.
< = > 2x3 : x -2 + 4x6 : x -2
< = > 2x3 : 1/ x2 + 4x6 : 1/ x2
< = > 2x3 . x2 + 4x6 . x 2
< = > 2 x3 + 2 + 4 x6 + 2
< = > 2 x5 + 4x8
2. Tentukan hasil dari bentuk pangkat berikut :
a. 53 x 54
b. ( -3 ) 6 x ( -3 ) 9
c. ( – 2 ) 10 x ( -2 ) 20
d. a10 x a20 x a30
Penyelesaian :
a. 53x 54 = 5 3+ 4 = 57
b. ( -3 )6x ( -3 )9 = ( – 3 ) 6 + 9 = ( – 3 ) 15
c. ( – 2 )10x ( -2 ) 20 = ( -2 ) 10 + 20 = ( -2 ) 30
d. a10x a20x a30 = a 10 + 20 + 30 = a 60
Demikian penjelasan mengenai Pengertian dan sifat – sifat bilangan berpangkat . Intinya , dalam bilangan berpangkat , ada hubungan antara penjumlahan , pengurangan , perkalian dan pembagian . Dan supaya dalam mengerjakan soal bilangan berpangkat menjadi lebih mudah , maka anda semua harus memahami betul mengenai sifat – sifat bilangan berpangkat . Jika anda sudah memahaminya , maka di buat dalam bentuk apa pun akan terasa mudah . Semoga dengan penjelasan dan contoh di atas , kita semua akan bertambah ilmunya . Serta dapat membantu permasalahan dalam materi bilangan berpangkat .
Mengenal Rumus Segitiga Istimewa Dalam Matematika
Rumus Segitiga Istimewa | Rumus segitiga istimewa merupakan pengembangan dari rumus pythagoras dalam segitiga siku – siku . Segitiga apa sajakah yang termasuk kedalam segitiga istimewa ? dan bagaimana rumusnya ? kali ini , kita akan mempelajarinya bersama .
Masih ingatkah kalian mengenai rumus pythagoras dan apa fungsinya ? ya betul sekali , rumus pythagoras digunakan untuk menghitung atau mencari panjang salah satu sisi segitiga siku – siku . Selain itu juga , teorema pythagoras juga dapat digunakan untuk menghitung perbandingan sisi – sisi pada segitiga istimewa .
Rumus Segitiga Istimewa
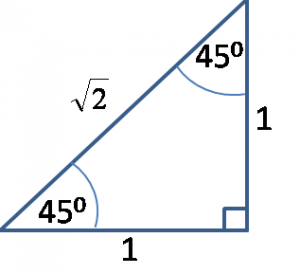
- Segitiga Siku – siku sama sisi ( segitiga sudut 45° )
Perhatikan gambar dibawah ini :
Segitiga ABC di atas merupakan segitiga siku – siku sama sisi , dengan sudut siku – siku di B dan ∠CAB= ∠BCA = 45° dan panjang BC = 2x . Dengan demikan , panjang BC = AB , dan BC = 2x . Lalu berapakah panjang AC ?
Untuk mecari panjang AC , maka kita masukkan pada rumus pythagoras sebagai berikut :
AC = √ BC2 + AB2
= √2x2 + 2x2
= √8x2
=2x √2
Maka dihasilkan , rumus sbb :
perbandingan sisi – sisi pada segitiga siku – siku sama sisi adalah tinggi : alas : sisi miring = 1 : 1 : √2
atau rumus cepat nya adalah :
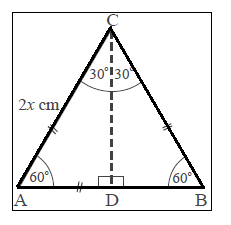
2. Segitiga siku – siku dengan sudut 30°, 90°, 60°
Perhatikan gambar di bawah ini :
Segitiga ACB diatas merupakan segitiga sama sisi , dan apabila di potong menjadi dua menghasilkan dua segitiga siku – siku yaitu ∆ ADC , Siku – siku di D dan ∆ BDC , siku – siku di D juga . dan di hasilkan juga ∠CAD = ∠CBD =60° , ∠ACD = ∠BCD = 30° , ∠ADC = ∠BDC = 90° . Serta diketahui panjang AC = 2x . Kali ini , kita fokuskan pada ∆ ADC yang telah diketahui panjang AC = 2x , untuk mencari AD dan CD kita gunakan rumus pythagoras sebagai berikut :
CD = √ AC2 – AD2
= √ 2x2 – x2
= √ 4x2 – x2
= √ 3x2
CD = x √ 3
Maka di hasilkan rumus :
Jadi , perbandingan segitiga istimewa dengan sudut 30°, 90°, 60° adalah alas : tinggi : sisi miring = 1 : √3 : 2
atau rumus cepatnya adalah :
Contoh Soal :
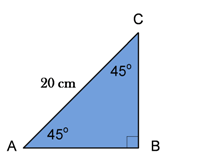
- Perhatikan gambar segitiga siku – siku dibawah ini :
Tentukan panjang AB , apabila diketahui panjang AC = 20 cm !
Penyelesaian :
Diketahui AC = 20cm ,
Ditanya AB = . . . .?
Jawab :
Gunakan Rumus :
maka AB = 1/2 a√2
= 1/2 . 20√2
AB = 10√2
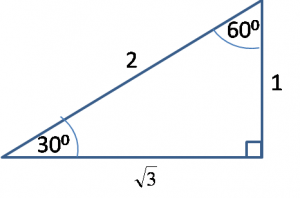
2. Perhatikan gambar di bawah ini :
Tentukan panjang CB dan AB , apabila diketahui panjang AC = 12√3 !
Penyelesaian :
Diketahui AC = 12√3
Ditanta CB dan AB = . . . ?
Jawab :
ingat rumus di bawah ini :
maka dihasilkan :
CB = 1/2 . a√3
= 1/2 . 12√3 .√3
= 1/2 .12 . 3
= 18 cm
AB = 1/2.a
=1/2 . 12√3
= 6√3 cm
3. Perhatikan gambar di bawah ini :
Gambar di atas merupakan bangun persegi yang terbelah menjadi 2 segitiga , dengan panjang garis potong ( AC) =10cm , dan ∠CAB = 45°. Maka tentukan :
a. panjang AB
b. Luas persegi ABCD
c. Keliling persegi ABCD
Penyelesaian :
a. Panjang AB = . . .?
gunakan rumus :
AB = 1/2 . a√2
AB = 1/2 . 10√2
AB = 5√2
b. Luas persegi ABCD = s x s
= 5√2 x 5√2
= 50 cm2
c. Keliling Persegi ABCD = 4s
= 4 (5√2 )
= 20 √2
4. Sebuah ∆ ADC , dengan ∠DAC = 60°. dan panjang AC = 14cm . Tentukan panjang AD !
Penyelesaian :
masukan ke rumus :
di misalkan AC = a , AD = 1/2a√3
maka di hasilkan
AD = 1/2a√3
AD = 1/2 . 14√3
AD = 7√3 cm
Demikian penjelasan mengenai Rumus Segitiga Istimewa dalam matematika . Semoga dengan penjelasan yang singkat , kalian semua sapat memahami apa saja yang termasuk segitiga istimewa beserta dengan rumusnya . Inti dari rumus segitiga istimewa adalah prisipnya sama dengan teorema pythagoras . Dan fahami tentang sudutnya apakah segitiga tersebut bersudut 30°, 60°, 90° ataukah bersedut 45 °, 45°, 90° .Jika sudah menguasai rumus pythagoras dan memahami sudut – sudutnya maka akan mudah dalam mengerjakan soal segitiga istimewa . Semoga bermanfaat .


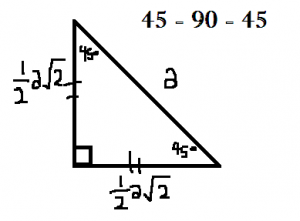
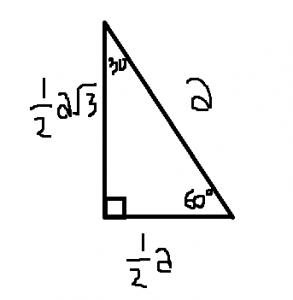
0 Response to "√Memahami Macam – Macam Pola Bilangan Dalam Matematika Lengkap Kuncinya"
Posting Komentar