√Cara Cepat Memahami Himpunan Semesta Dan Himpunan Bagian Lengkap Kuncinya

Cara Cepat Memahami Himpunan Semesta Dan Himpunan Bagian

Memahami Hipunan Semesta dan Himpunan Bagian | Materi Himpunan semesta dan himpunan bagian merupakan salah satu materi dalam ilmu matematika yang dipelajari sejak SD . Himpunan merupakan suatu kumpulan objek atau benda yang dapat di definisikan secara jelas . Didefinisikan secara jelas yaitu jelas keanggotaannya yaitu setiap kita tunjuk objek , kita dapat mengatakan dengan tegas anggotanya atau bukan anggotanya . Lalu apakah yang dimaksud dengan himpunan semesta dan himpunan bagian ? Pada kesempatan kali ini , kita akan mempelajarinya serta memahami bagaimana cara mengerjakan apabila ada suatu permasalahan yang berhubungan dengan himpunan semesta ataupun himpunan bagian .

Himpunan Semesta dan Himpunan Bagian

Sebelum mempelajari himpunan semesta dan himpunan bagian , maka terlebih dahulu mempelajari himpunan bilangan , perhatikan penjelasan di bawah ini .

Himpunan Bilangan meliputi :

a. Himpunan Bilangan Asli ( A )

A = { 1 , 2 , 3 , 4 , . . . . }

b. Himpunan Bilangan Cacah ( C )

C = { 0 , 1 , 2 , 3 , 4 , 5 , . . . .}

c. Himpunan Bilangan Bulat ( B )

B = { . . . ., -3 ,-2 ,-1 , 0 ,1  , 2 , 3 , . . . }

d. Himpunan Bilangan Rasional ( Q )

Q = { x / x = a/b , a dan b ∈ B , b ≠ 0 }

• Dalam ilmu matematika , tidak mempelajari bilangan yang di bagi 0 . , jadi 0 / o dijawab berapapun benar .
• Bilangan Rasional meliputi bilangan bulat dan pecahan .

e. Himpunan Bilangan Prima ( P )

Bilangan prima yaitu bilangan yang tepat dua buah .

P = { 2, 3 , 5 , 7 , 11 , 13 , 17 . 19 , 23 , 29 , 31 , 37 , 41 , 43 , 47 . . . dst }

Cara Menyatakan Himpunan 

Ada tiga macam cara untuk menyatakan himpunan , yaitu :

a. Dengan menggunakan kata – kata

Contoh :

• Himpunan bilangan prima yang kurang dari 10
• Himpunan huruf Vokal

b. Dengan Cara menuliskan anggotanya

Contoh :

• A = { 2 , 3 , 5 , 7 }
• V = { a , i , u , e , o }

c. Dengan Cara menggunakan notasi pembentuk himpunan

Contoh :

A = { x / x < 10 , x bilangan prima }

Jika dibaca adalah A adalah himpunan semua x sedemikian hingga x kurang dari 10 dan x bilangan prima .

Himpuna semesta 

Himpunan semesta yaitu himpunan yang memuat semua anggota yang sedang dibicarakan . Himpunan semesta dilambangkan dengan huruf  ” S ” .

Contoh 1 :

A = { 1 , 2, 3 , 5 , 7 }

B = {  5 , 7 , 9 }

S = { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 }

Irisan Himpunan (  )

Irisan Himpunan , dimisalkan A    B yang artinya bahwa himpunan yang anggotanya menjadi nggota A , dan sekaligus menjadi anggota B .

Contoh 2:

A = { 1, 2 ,3 , 4 }

B= { 3 , 4 , 5 }

A    B = { 3 , 4 }

Gabungan (  )

Gabungan , dimisalkan A   B Yang artinya bahwa himpunan yang anggotanya menjadi anggota A atau menjadi anggota B .

Contoh 3:

A = { 1, 2 ,3 , 4 }

B= { 3 , 4 , 5 }

A   B = { 1, 2 , 3 , 4 , 5 }

Diagram Venn

Suatu himpunan dapat dinyatakan dalam diagram ven , diagram ven merupakan diagram yang pertama kali dikemukakan oleh ilmuwan asal Inggris yang bernama JHON VENN .

Dalam diagram venn , himpuan semesta dinyatakan dengan benuk persegi panjang . Sedangkan himpunan yang lain , di luar semesta dinyatakan dalam kurva sederhana dan noktah – noktah untuk menyatakan anggotanya . Dan apabila tidak ada himpunan yang sama antara himpuna A dan B , maka lingkaran dalam himpunan semesta tersebut tidak saling berpotongan . Untuk lebih jelasnya perhatikan contoh di bawah ini

Contoh 4 :

1.) S = { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 }

A = { 1 , 4 , 6 , 7 }

B = { 2 , 4 , 5 , 8 }

A    B = { 4 }

A   B = { 1 , 2 , 4 , 5  , 6 , 7 , 8 }

Maka apabila digambarkan dalam diagram VENN , adalah :

2.) S = { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 }

 X = { 1, 2 , 4 , 5 }

Y = { 6 , 7 , 8 }

Himpunan Kosong  ( { } )

Himpunan kosong adalah himpunan yang tidak memiliki anggota , dan dinotasikan dengan { } atau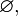 

Himpunan kosong ( { } ) , merupakan himpunan bagian dari setiap himpunan .

Himpunan Bagian  ( ⊂  )

Himpuna bagian dimisalkan dengan A ⊂  B , Artinya jika setiap anggota A ( Semua anggota A ) , Menjadi anggota B .

Contoh 5:

1.) A = { 1 , 2 , 3 }

B = { 0 , 1 ,2 , 3 , 4 }

A ⊂  B , Karena semua anggota A Menjadi anggota B .

2.) P = { a , b , c }

Q = { a , c , d , e , f }

P bukan Himpunan bagian dari Q ( P ⊂ Q ) , Karena ada anggota P yang tidak menjadi anggota Q .

3.) P = { a , b , c } , Tulislah semua himpunan bagian dari P

1. { }
2. { a }
3. { b }
4. { c }
5. { a , b }
6. { a , c }
7. { b , c }
8. { a , b , c }

“Catatan : Setiap himpunan , merupakan himpunan bagian dari himpunan itu sendiri “

Dari contoh nomor 3 , maka Cara untuk menentukan Banyaknya Himpunan Bagian A , maka Rumusnya adalah :

A  = 2 n(A)

Keterangan :

n(A ) = Banyaknya anggota A

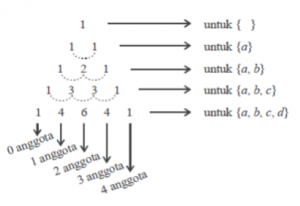
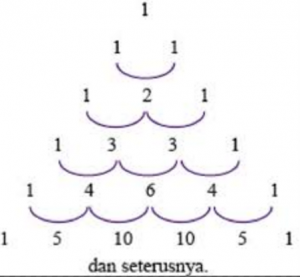
Untuk menentukan banyaknya himpunan bagian suatu himpunan ,yaitu dengan menggunakan konsep segitiga pascal . Perhatikan gambar di bawah ini :

4.)  P ={ 0 , 1 , 2 , 3 , 4 } , n ( P ) = 5

a. Tentukan banyaknya himpunan bagian P

b. Tentukan Banyaknya Himpunan Bagian P yang mempunyai 3 anggota .

Penyelesaian :

a. Banyaknya Himpunan Bag. P = 2 n(P)

                                                          = 2 5     = 32

b. Banyaknya Himpunan Bagian P yang mempunyai 3 anggota adalah 10  ( caranya melihat segitiga pascal berikut)

Komplemen Suatu Himpunan 

Komplemen suatu himpunan Dimisalkan dengan AC atau  Al, yaitu himpunan yang anggotanya adalah anggota S selain anggota  A 

Untuk lebih memahaminya , perhatikan contoh berikut

Contoh 6 :

1.) S = { 0 ,1 ,2 ,3 ,4 ,5 }

A = { 1 , 2 , 3 , 4 }

Maka dihasilkan AC  = { 0 , 5 } dan ( AC )C  =  { 1 , 2 , 3 , 4 }

atau dengan kata lain ( AC )C = A

2.) S = { 0 , 1 , 2 ,3 ,4 , 5 , 6 , 7 , 8 , 9 }

P = { 2 , 3 , 4 , 5 }

Q = { 4 , 5 , 6 , 7 , 8 }

Tentukan :

a. P    Q

b. P   Q

c. PC  

d. QC  

e. ( P    Q )C

f. ( P   Q )C

g. PC    QC  

h. PC    QC  

Penyelesaian :

a. P    Q = { 4 , 5 }

b. P   Q = { 2 , 3 , 4 , 5 , 6 , 7 , 8 }

c. PC  = { 0 , 1 , 6 , 7 , 8 , 9 }

d. QC   = { 0 , 1 , 2 , 3 , 9 }

e. ( P    Q )C = { 0 , 1 , 2 , 3 , 6 , 7 , 8 , 9 }

f. ( P   Q )C = { 0 , 1 , 9 }

g. PC    QC   = { 0 , 1 , 9 }

h. PC    QC   = { 0 , 1 , 2 , 3 , 6 , 7 , 8 , 9 }

Dari Contoh di atas maka , dihaslkan rumus sebagai berikut :

( P    Q )C   =  PC    QC

( P   Q )C  =   PC    QC   

          atau 

( A    B )C   =AC    BC

( A   B )C  =  AC    BC

Demikian penjelasan mengenai Cara cepat untuk memahami Himpunan Semesta Dan Himpunan Bagian Dari suatu bilangan dalam ilmu matematika . Semoga dengan penjelasan di atas , dapat membantu anda dalam mengerjakan soal himpunan dan semua yang masalah yang termasuk di dalamnya . Semoga ilmu kita bermanfaat . Amin

Memahami Rumus Persamaan Kuadrat Dalam Ilmu Matematika

Rumus Persamaan Kuadrat | Rumus persamaan kuadrat merupakan rumus untuk menyelesaikan suatu bentuk persamaan kuadrat . Bagaimanakah cara untuk menyelesaikannya ? Sebelum mengetahui bagaimana cara untuk menyelesaikannya , kita harus mengetahui terlebih dahulu mengenai pengertian persamaan kuadrat .

Persamaan Kadrat adalah Suatu bentuk persamaan polinomial berpangkat dua .

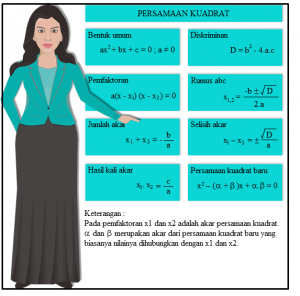
Bentuk umum persamaan kuadrat :

Keterangan :

a = koefisien kuadrat x

b = koefisisen linier x

c = suku bebas atau koefisien konstanta

Nilai koefisien a , b , dan c dalam Fungsi persamaan kuadrat :

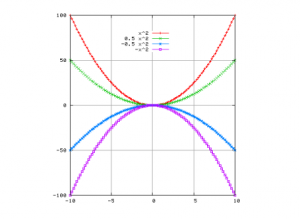
• Koefisien a , menentukan seberapa cekung atau cembung suatu parabola dalam fungsi persamaan kuadrat . Apabila a > 0 , maka parabola tersebut membuka ke atas . Dan apabila a < 0 , maka parabola akan terbuka ke bawah .

Perhatikan gambar di bawah ini :

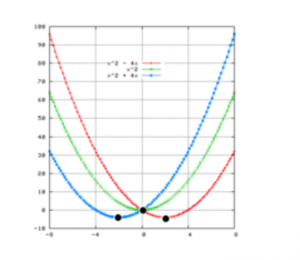
• Koefisien b , Menentukan posisi puncak x atau sumbu simetri dari sebuah kurva yang dibentuk . Posisi tepatnya yaitu  – b / 2a

Perhatikan Gambar di bawah ini :

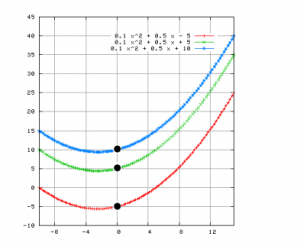
• KOefisien c , menentukan titik potong dari suatu bentuk persamaan dalam bentuk parabola yang dibentuk pada sumbu y , dimana x = 0

Perhatikan gambar di bawah ini :

Rumus Persamaan Kuadrat

Rumus persamaan kuadrat merupakan suatu cra untuk menyelesaikan sebuah permasalahan persamaan kuadrat . Berikut adalah Cara – cara  untuk menyelesaikan persamaan kuadrat :

1. Memfaktorkan 

Memfaktorkan yaitu cara menyelesaikan persamaan kuadrat dengan cara mencari 2 bilangan yang merupakan faktor  dari bentuk persamaaan tersebut . Bentuk umum dari persamaan kuadrat  ax2 + bx + c = 0 , dengan a≠0

<=> ( x – a ) ( x – b ) atau ( x – a ) ( x + b )

Caranya yaitu mencari 2 angka yang apabila di jumlahkan hasilnya b , dan apabila dikalikan hasilnya c .

Contoh :

Tentukan himpunan penyelesaian dari bentuk persamaan x2 – 2x – 8 = 0

Penyelesaian:

x2 – 2x – 8 = 0 , faktor dari persamaan tersebut adalah ( 2 , -4 )

x2 – 2x – 8 = 0

< = > ( x + 2 ) ( x -4 )

Jadi HP = { 2 , -4 }

2. Melengkapi Kuadrat Sempurna 

Langkah – langkah dalam melengkapi kuadrat menjadi bentuk kuadrat sempurna :

a. Koefisien x2  harus 1

b. Konstanta pindah ke ruas kanan

c. Di ubah kebentuk kuadrat sempurna

Contoh :

Tentukan himpunan penyelesaian dari bentuk persamaan x2 – 2x – 8 = 0

Penyelesaian :

x2  + 2x  – 8 = 0

<= > x2  + 2x  = 8 , memindahkan kontanta ke sebelah kanan , setelah itu mencari 1/2 dari konstanta untuk menjadikan kuadrat menjadi sempurna .

< =>  x2  + 2x  + ( 1/2 .2 )2 = 8 + ( 1/2 .2 )2

<= >   x2  + 2x + 1 = 8 + 1

< = >   x2  + 2x + 1= 8 + 1

< = > x2  + 2x + 1= 9

< = > ( x + 1 ) 2 = 9

<=> x + 1 = ± √9

< =>  x + 1 = ± 3

< = >  x + 1 =  3 , atau x + 1 = – 3

< = > x = 3 – 1 , x = -3 -1

< = > x = 2 , x = -4

Maka HP = { 2 , -4 }

3. Menggunakan Rumus ABC  ( Rumus Kuadratis )

Contoh :

Tentukan himpunan penyelesaian dari bentuk persamaan x2 – 2x – 8 = 0

Penyelesaian :

x2 – 2x – 8 = 0 , lalu menuliskan rumus abc

<=>x1 ,2 = – b  ± √b2  – 4ac / 2.a

<=>x1 ,2 = 2 ± √4 + 32 /2

<=>x1 ,2  = 2 ± 6 /2

<=> x1,2 = (2+6)/2  atau  x1,2 = (2-6)/2

<=> x1 = 4 , atau x2 = -2

Jadi HP = { 4 , -2 }

Mengapa di sebut dengan rumus abc ? Karena rumus tersebut digunakan untuk menghitung akar – akar dari a,b dan c . Dalam rumus abc ini , terdapat sebuah istilah yaitu diskriminan atau determinan . Diskriminan atau determinan memiliki arti  tanda akar  b²-4ac , atau dilambangkan dengan huruf ” D ” .

Suatu koefisien riil dalam persamaan kuadrat ,dapat hanya memiliki satu akar atau dua akar yang berbeda dan akar – akar tersebut dapat berbentuk bilangan riil atau kompleks . Diskriminan , dapat menentukan jumlah banyaknya akar dari persamaan tersebut . Berikut adalah kemungkinan – kemungkinan yang dapat terjadi :

• Apabila diskriminan bernilai positif , maka akan terdapat dua akar yang berbeda dan merupakan bilangan riil . Dan apabila koefisien dalam persamaan tersebutmerupakan bilangan bulat , dan diskriminan nya berupa bilangan kuadrat sempurna , maka akar – akar dari persamaan tersebut berupa bilangan rasional atau bisa juga berupa bilangan irasional .
• Apabila diskriminan dari persamaan tersebut bernilai nol , maka akarnya berupa satu bilangan riil .Dan di sebut sebagai akar ganda ,

akar ganda , yaitu :

• Apabila diskriminan bernilai negatif dan tidak terdapat bilangan riil . Sebagai gantinya , terdapat dua buah akar kompleks yang disebut juga sebagai konjugat kompleks. Berikut adalah bentuk dari konjugat kompleks:

Rumus Yang perlu untuk difahami dan Diingat dalam Persamaan Kuadrat :

1. Bentuk Umum persamaan Kuadrat :

ax2 + bx + c = 0 , dengan a≠0

2. Pemfaktoran

( x – x1 ) ( x – x2 ) = 0

3. Jumlah Akar

x1 + x2 = -b / a

4. Hasil kali akar

x1 . x2 = c / a

5. Selisih akar

x1 – x2 = ± √D /4

6. Diskriminan

D = b2 – 2a.c

7. Rumus ABC

x1 , 2 = – b  ± √D / 2.a

8. Persamaan Kuadrat Baru

x2 – ( a +β ) x + a . β = 0

Demikian penjelasan mengenai rumus persamaan kuadrat . Pada dasarnya , operasi hitung yang dipakai dalam persamaan kuadrat yaitu sama dengan operasi hitung matematika yang lainnya yaitu mengenai penjumlahan , pengurangan , perkalian dan pembagian . Serta kita juga harus faham inti dasar dari persamaan kuadrat tersebut , serta tidak lupa untuk sering – sering latihan mengerjakan soal – soal yang berhubungan dengan persamaan kuadrat. Inti dasar dari persamaan kuadrat adalah , memahami bahwa bentuk persamaan kuadrat secara umum adalah ax2 + bx + c = 0 dimana a bukan 0 . Semoga dapat sedikit menambah pengetahuan mengenai rumus persamaan kuadrat .

Rumus Bangun RuangSisi Tegak Dalam Matematika

Rumus Bangun Ruang Sisi Tegak |Apakah perbedaan dari rumus bangun ruang sisi lengkung dengan bangun ruang sisi tegak ? kali ini kita akan mempelajari bersama . Sebelum mempelajari itu semua , pertama kali harus mengetahui pengertian bangun ruang  .

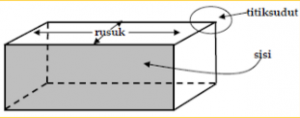
Bangun ruang merupakan suatu istilah untuk bangun matematika tiga dimensi yang memiliki panjang lebar dan tinggi atau bangun yang terdiri dari tiga unsur yaitu  sisi , rusuk , titik sudut , diagonal sisi dan diagonal ruang .

• Sisi yaitu bagian suatu bangun yang membatasi bagian dalam dan luar .
• Rusuk yaitu perpotongan dua bidang sisi suatu bangun.
• Titik sudut yaitu Perpotongan tiga sisi atau rusuk .

Untuk lebih jelasnya perhatikan gambar di bawah ini :

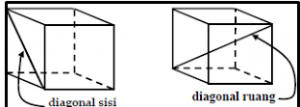
• Diagonal sisi , yaitu suatu garis yang melintang yang menghubungkan dua buah titik sudut yang letaknya tidak berurutan dalam sisi sebuah bangun dan letaknya berhadapan .
• Diagonal Ruang , yaitu  sebuah garis pada bangun ruang yang menghubungkan dua buah titik sudut yang berhadapan serta tidak berurutan .

Untuk lebih jelasnya perhatikan gambar di bawah ini :

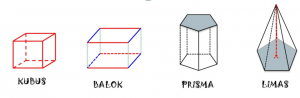
Bangun Ruang terbagi menjadi dua macam , yaitu :

1. Bangun Ruang sisi Tegak , yaitu terdiri dari kubus , balok , prisma dan limas
2. Bangun Ruang sisi Lengkung , yaitu terdiri dari tabung , kerucut dan bola

Pada kesempatan kali ini , yang akan kita pelajari adalah rumus bangun ruang sisi tegak .

Rumus Bangun Ruang Sisi Tegak

1. Kubus 

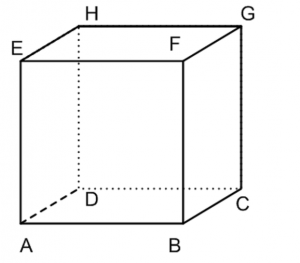
Kubus yaitu bangun ruang yang memiliki sisi yang sama dan rusuk sama panjang .

Kubus terdiri dari 6 buah bidang sisi / bidang , 8 buah titik sudut dan 12 rusuk .

Perhatikan gambar di bawah ini :

Jaring – jaring kubus:

• Luas Permukaan Kubus 

Dalam sebuah kubus terdiri dari 6 bidang yang berbentuk segi empat . Sedangkan luas persegi = sisi x sisi (  s2 ), jadi luas permukaan kubus adalah 6 kali luas persegi .

• Volume Kubus

Kubus merupakan bangun ruang yang memiliki panjang rusuk sama panjang , maka dalam kubus tidak ada istilah panjang ( p ) , lebar ( l ) dan tinggi ( t ) . Namun itu semua diganti dengan sisi ( s )

Jadi , volume kubus adalah :

Volume = Luas alas x tinggi

= s x s x s

= s3

Jadi , Rumus Volume Kubus adalah :

2. Balok 

Balok merupakan bangun ruang atau bangun tiga di mensi yang bentuknya hampir sama dengan kubus , yang membedakan hanyalah ukuran rusuknya , pada kubus sama panjang sedangkan pada balok berbeda panjangnya .

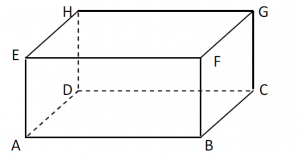
Perhatikan Gambar di bawah ini :

Setelah kita lihat gambar di atas , maka dapat kita fahami ada sisi yang kongruen . Sisi – sisi tersebut adalah :

• Sisi ABEF ,kongruen dengan sisi CDGH ( sisi depan dan belakang )
• Sisi BCFG , kongruen dengan sisi ADEH ( sisi samping kiri dan kanan )
• Sisi ABCD , Kongruen dengan sisi EFGH ( sisi atas dan bawah )

Kongruen yaitu sama dan sebangun baik panjang ataupun sudutnya .

Jaring – jaring balok 

Balok terdiri atas  6 bidang sisi , 12 rusuk dan 8 titik sudut .

• Luas Permukaan Balok 

Balok terdiri dari 3 sisi yang saling berhadapan ,yaitu

1. Sisi ABEF ,kongruen dengan sisi CDGH ( sisi depan dan belakang )
2. Sisi BCFG , kongruen dengan sisi ADEH ( sisi samping kiri dan kanan )
3. Sisi ABCD , Kongruen dengan sisi EFGH ( sisi atas dan bawah )

Rumus untuk mencari luas permukaan balok adalah :

Luas ABCD  = P x L

Luas ABEF  = Px t

Luas BCFG  = L x T

Luas Balok = 2( p x l ) + 2( p x t ) + 2( l x t )

= 2 (p x l + p x t + l x t )

Jadi , Rumus Luas permukaan Balok adalah

•  Volume Balok 

Volume balok = La x t

= p x l x t

Jadi , rumus volume balok adalah

3. Prisma 

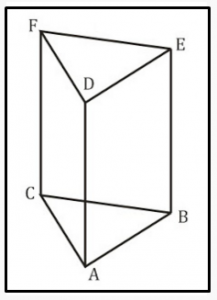
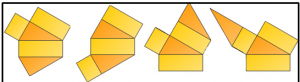
Prisma yaitu bangun ruang atau bangun tiga dimensi yang memiliki dua buah bangun yang kongruen dan saling berhadapan , dua bangun yang berhadapan tersebut disebut sebagai alas dan tutup , sedangkan yang menghubungkan ke dua bangun tersebut  disebut dengan tinggi  . Atau dapat di lihat dari ciri – ciri lain , bahwa prisma adalah bangun ruang yang terdiri dari sisi yang berbeda yang saling berpotongan pada titik – titik sudut .  Untuk lebih jelasnya perhatikan gambar di bawah ini :

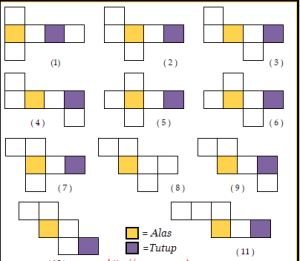
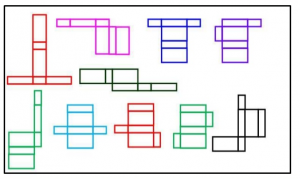
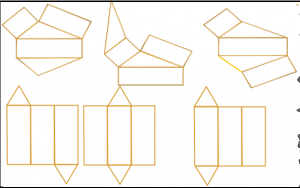
Berikut adalah beberapa contoh Jaring – jaring prisma :

• Luas Permukaan Prisma 

Luas permukaan prisma , yaitu jumlah luas alas , luas tutup dan luas sisi tegak .

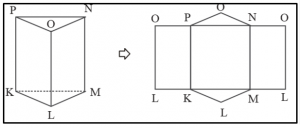
Perhatikan gambar prisma di bawah ini :

Luas permukaan prisma = ( Luas KLM + Luas NOP ) + ( Luas KLOP + Luas KMNP + Luas LMNO )

= ( 2 x Luas KLM ) + { ( LK x t ) + ( KM x t ) + ( LM x t ) }

= ( 2 x Luas alas ) +  t ( LK + KM + LM )

= ( 2 x Luas alas ) + t x Keliling alas

Jadi , Rumus Luas permukaan prisma adalah :

Luas Permukaan Prisma = ( 2 x Luas Alas ) + t x Keliling alas 

• Volume Prisma 

Untuk menghitung volume prisma , yaitu harus memperhatikan alasnya . Karena rumus volume prisma tergantung dengan bentuk alasnya.

Volume prisma segi tiga =( 1/2 x alas x tinggi segitiga ) x tinggi prisma

Volume prisma segi empat = ( s x s ) x tinggi prisma

dan lain sebagainya . Dan dapat disimpulkan bahwa ruus volume prisma adalah :

Volume prisma = Luas Alas x Tinggi

4. Limas 

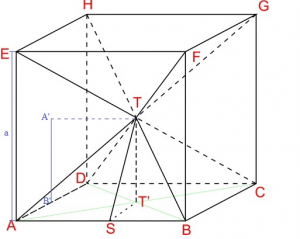
Limas merupakan bangun 3 dimensi yang memiliki sisi miring berbentuk segi tiga dan memiliki titik puncak . Tahukah anda , bahwa kubus adalah gabungan dari 6 buah limas ? perhatikan gambar di bawah ini :

Dari gambar di atas , ada 6 buah limas dengan titik puncak T dan membentuk sbuah kubus .

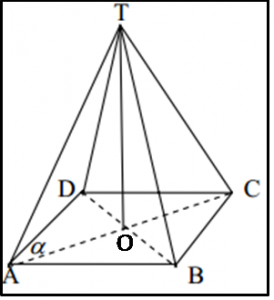
Untuk lebih jelasnya mengenai bentuk limas , perhatikan gambar di bawah ini :

• Luas Permukaan Limas 

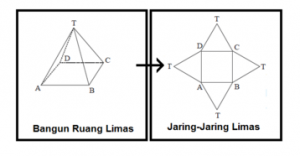
Untuk dapat menyelesaikan atau cara untuk mencari luas permukaan limas , pertama kali kita harus memahami jaring – jaring dari limas tersebut . Karena hal itu akan membantu untuk mengetahui rumus luas permukaan limas . Perhatikan gambar di bawah ini :

Dari gambar di atas , diketahui bahwa alas bangun limas tersebut berbentuk persegi empat . Jadi , rumus untuk mencari luas permukaan limas adalah :

Lpermukaan limas = L uas ABCD +( Luas ∆TAB + Luas ∆TBC + Luas TCD + Luas ∆TAD)

= Luas alas + Jumlah Luas Sisi tegak

Jadi , Rumus permukaan limas adalah :

Luas Permukaan = Luas alas + Jumlah luas Sisi Tegak

• Volume Limas 

Untuk dapat memahami bagaimana rumus volume limas , maka terlebih dahulu perhatikan gambar di bawah ini :

Luas  alas = p x l     ( karena alasnya berbentuk persegi panjang )

Luas alas = s x s      ( apabila alasnya berbentuk persegi empat )

Demikian penjelasan mengenai rumus bangun ruang sisi tegak , pada dasarnya untuk dapat memudahkan dalam memahami dan hafal mengenai rumus bangun ruang sisi tegak yaitu dengan memahami bentuk – bentuknya apakah bangun ruang sisi tegak ataukah bangun ruang sisi lengkung dan sering – seringlah untuk latihan mengerjakan dan dengan sendirinya akan hafal .

 

Tweet

Subscribe to receive free email updates: