Dalil Pythagoras Dalam Ilmu Matematika
Dalil Pythagoras |Dalil pythagoras sering dikenal dengan istilah teorema pythagoras . Kalimat pythagoras pasti sudah tidak asing lagi di telinga kita,karena sejak SD ketika pembelajaran matematika pasti kita tidak ketinggalan untuk mempelajari pytagoras . Rumus pythagoras merupakan rumus yang ditemukan oleh ilmuwan yunani yang bernama pythagoras.
Pengertian dari teorema pythagoras atau dalil pythagoras yaitu bahwa sisi miring atau sisi terpanjang dalam segitiga siku – siku sama dengan kuadrat sisi – sisi lainnya.
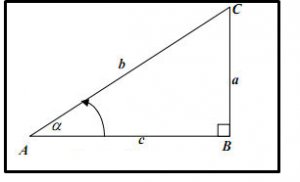
Perhatikan gambar di bawah ini:
Segitiga di atas merupakan segitiga siku-siku yang memiliki satu sisi tegak (BC),satu sisi mendatar (AB)dan satu sisi miring (AC).Dalil pythagoras atau rumus pythagoras berfungsi untuk mencari salah satu sisi dengan kedua sisi diketahui.
Rumus Pythagoras :
b2 = a2 + c2
maka untuk menghitung sisi tegak dan sisi mendatarnya berlaku rumus :
a2 = b2 – c2
c2 = b2 – a2
Rumus Pythagoras dalam bentuk akar , jika sisi miringnya c , sisi tegak dan mendatarnya adalah a dan b , maka rumus yang dihasilkan :
Rumus pythagoras , hanya berlaku pada segitiga siku – siku saja .
Dalam dalil /teorema pythagoras , ada pola angka yang perlu untuk diingat supaya dalam menyelesaikan soal pythagoras akan lebih mudah dan cepat dalam mengerjakannya , pola tersebut adalah :
- 3 – 4 – 5
- 5 – 12 – 13
- 6 – 8 – 10
- 7 – 24 – 25
- 8 – 15 – 17
- 9 – 12 – 15
- 10 – 24 – 26
- 12 – 16 – 20
- 14 – 48 – 50
- 15 – 20 – 25
- 15 – 36 – 39
- 16 – 30 – 34
Untuk memahami lebih jelasnya mengenai dalil pythagoras , maka perhatikan contoh sebagai berikut
Contoh soal :
- Suatu segitiga siku- siku memiliki sisi tegak (AB) panjangnya 15 cm ,dan sisi mendatarnya (BC) 8 cm ,berapakah cm kah sisi miringnya (AC) ?
Penyelesaian :
Diketahui :
AB = 15
BC = 8
Ditanya :
panjang AC …???
Jawab :
Cara pertama :
AC2 = AB2 + BC2
= 152 + 82
= 225 + 64
= 289
AC =√289
AC = 17
Cara kedua :
AC = √ AB2 + BC2
AC = √ 152 + 82
AC = √ 255 + 64
AC = √ 289
AC = 17
Jadi, panjang AC adalah 17cm
- Berapakah panjang sisi tegak suatu segitiga siku – siku apabila diketahui panjang sisi miringnya 13 cm dan sisi datarnya 5 cm ?
penyelesaiaannya :
Misal : c = sisi miring , b = sisi datar , a = sisi tegak
Diketahui : c = 13 cm , b = 5 cm
Ditanya : a = ….????
Jawab :
Cara pertama :
a2 = c2 – b2
= 132 – 52
= 169 – 25
= 144
a = √ 144
a = 12
Cara kedua :
a = √ c2 – b2
= √ 132 – 52
= √ 169 – 25
= √ 144
= 12
Jadi, panjang sisi tegak segitiga tersebut adalah 12 cm
3. Ada sbuah segitiga ABC , siku – siku di B . Apabila panjang AB = 16 cm dan BC = 30 , maka berapakah panjang sisi miring segitiga tersebut ( AC ) ?
Penyelesaian :
Diketahui :
AB = 16
BC = 30
Ditanya : AC = . . . ?
Jawab :
AC = √ AB2 + BC2
= √ 16 2 + 302
=√ 256 + 900
AC = √ 1156
= 34
Jadi , panjang AC = 34 cm
Demikian penjelasan tentang dalil pythagoras , semoga bermanfaat dan bisa membantu dalam belajar matematika yang sering membuat sebagian dari kita pusing tujuh keliling,padahal aslinya jika kita mempelajari dengan tekun maka semua hal yang sulit akan menjadi mudah. Inti dari rumus dalil pythagoras adalah sisi miring sama dengan sisi tegak di tambah sisi mendatar ( akan tetapi jangan lupa untuk dikuadratkan ). Good luck
Memahami Rumus Perbandingan Senilai Dan Berbalik Nilai
Memahami Rumus Perbandingan Senilai | Rumus perbandingan senilai dan berbalik nilai merupakan suatu cara aritmatika untuk menyelesaikan suatu permasalahan . Lalu apakah yang dimaksud dengan perbandingan senilai dan berbalik nilai ? Apa perbedaa dari keduanya ? Mari kita pelajari bersama .
Secara umum,pengertian dari kata perbandingan yaitu selisih antara dua hal yang memiliki pola yang sama.
-
Perbandingan Senilai
Perbandingan senilai adalah perbandingan dari dua atau lebih besaran dimana suatu variabel bertambah , maka variabel yang lain bertambah pula atau disebut juga dengan perbandingan yang memiliki nilai yang sama.
Contoh kejadian yang termasuk dalam perbandingan senilai antaralain :
- Jumlah tabungan dengan waktu penyimpanan.
- Banyak barang dengan jumlah harga barang .
- Jumlah pekerja dengan jumlah upah yang dikeluarkan .
Rumus perbandingan senilai:
Cara lain :
jika a = x
maka b = b/a * x
-
Perbandingan berbalik nilai
Perbandingan berbalik nilai adalah perbandingan dari dua atau lebih besaran dimana suatu variabel bertambah , maka variabel yang lain berkurang atau turun nilainya.
Contoh kejadian yang termasuk perbandingan berbalik nilai antaralain :
- Banyaknya pekerja dengan waktu penyelesaian.
- Banyaknya hewan dengan waktu penghabisan makanannya.
Rumus perbandingan berbalik nilai :
Cara lain :
jika a = x
maka b = a / b * x
Perbedaan Persamaan senilai dan berbalik nilai
Persamaan senilai :
Apabila suatau variabel suatu kejadian bertambah , maka yang lainnya akan bertambah ( terjadi sejajar )
persamaan berbalik nilai :
Apabila suatu variabel bertambah , maka yang lainnya akan berkurang ( terjadi kebalikannya )
Contoh soal
- Suatu rumah dikerjakan oleh 6 pekerja ,menghabiskan biaya untuk menggajihnya sebesar Rp 300.000 ,00 . Akan tetapi , pemilik rumah akan mempercepat waktu penyelesaiannya maka pekerja ditambah menjadi 8 orang,berapakah jumlah uang yang dikeluarkan untuk menggajinya ?
Penyelesaian :
Diketahui :
a1 = 6 , b1 =300.000 , a2 = 8
Ditanya : b2 = … ???
Jawab :
Cara 1
a1 / b1 = a2 / b2
6 / 300.ooo = 8 / b2 ( lakukan perkalian silang )
b2 × 6 = 300000 × 8
b2 = 2400000 / 6
= 400.000
Cara2
a= 6 pkerja
b = 8 pekerja x = 300.000
a = x
b = b / a * x
6 pekerja = 300. 000
8 pekerja = 8 / 6 * 300.000
= 400.000
Jadi, jumlah uang yang harus dikeluarkan sebesar Rp 400.000 ,00
- Harga apel dipasar 5 kg 20.000 ,berapakah harga apel 8 kg ?
Penyelesaian :
Diketahui : a1 = 5 , a1 = 20.000 , b1= 8
Ditanya : b2 = …???
Jawab :
Cara 1
a1 / b1 = a2 / b2
5 / 8 = 20.000 / b2 ( lakukan perkalian silang )
b2 = 20.000 x 8 / 5
b2 = 32.000
Cara 2
a= 5 pekerja
b = 8 pekerja
x = 20. 000
a = x
b = b / a * x
5 pekerja = 20. 000
8 pekerja = 8 / 5 * 20.000
= 32.000
Jadi, harga apel nya adalah Rp 32.000,00
- Suatu rumah dikerjakan oleh 8 pekerja,dan diselesaikan selama 15 hari. Apabila dikerjakan oleh 10 pekerja , berapa hari yang di butuhkan untuk menyelesaikan pekerjaan tersebut ?
Penyelesaian :
Diketahui :
a1 = 8 , b1 = 15 , a2 = 10
Ditanya : b2 = ….???
Jawab :
Cara 1
a1 / b2 = a2 / b1
8 / b2 = 10 / 15
b2 = 8 x 15 / 10
b2 = 12
Cara 2
a = 8 hari
b = 10 pekerja
x = 15 hari
a = x
b = a/b * x
8 pekerja = 15
10 pekerja = 8 / 10 * 15
= 12
Jadi waktu yang dibutuhkan adalah 12 hari
- 4 mesin dapat membuat sepatu selama 10 hari,jika yang digunakan sebanyak 8 mesin berapa kah waktu yang di butuhkan ?
Penyelesaian:
Diketahui :
a1 =4 , b1 = 10 , a2 = 8
Ditanya : b2 = …???
Jawab :
cara1
a1 / b2 = a2 / b1
4 / b2 = 8 / 10 ( lakukan perkalian silang )
b2 = 4 x 10 / 8
b2 = 5
cara 2
a= 4 mesin
b= 8 mesin
x = 10 hari
a = x
b = a / b * x
4 mesin = 10
8 mesin = 4 / 8 * 10
= 5
Jadi waktu yang dibutuhkan adalah 5 hari
5. Suatu rumah dikerjakan selama 15 hari oleh 8 pekerja. Apabila pemilik menginginkan selesai dalam waktu 12 hari , maka berapa pekerja yang perlu untuk ditambahkan ?
Penyelesaian
Diketahui :
a1 = 15 hari
b1 = 8 pekerja
a2 = 12 hari
Ditanya : jumlah pekerja yang ditambahkan = . . . ?
Jawab :
Cara 1
a1 / b2 = a2 / b1
15 / b2 = 12 /8
b2 = 15 x 8 / 12
b2 = 10
Cara 2
a = 15 hari
b = 12 hari
x = 8 pekerja
a = x
b = a / b * x
15 hari = 8
12 hari = 15 / 12 * 8
= 10
Jadi , jumlah pekerja yang harus di tambah = 10 – 8 = 2 pekerja
Contoh nomor 1 dan 2 adalah contoh perbandingan senilai , sedangkan nomor 3 , 4 dan 5 merupakan contoh perbandingan berbalik nilai .
Tips cara untuk menyelesaikan suatu persoalan perbandingan yaitu dengan cara memahami secara jeli,kuncinya adalah kita lihat apabila dalam suatu kejadian satu bertambah maka yang satu juga bertambah maka itu adalah perbandingan senilai.Dan apabila suatu kejadian bertambah ,tetapi yang lain berkurang maka hal itu dinamakan perbandingan berbalik nilai.Yang pasti kita harus sering untuk berlatih menyelesaikan soal – soal .
Demikian penjelasan tentang perbandingan senilai dan berbalik nilai ,semua persoalan akan terlihat mudah apabila kita menyukai dan berlatih berkali – kali.Maka dari itu ,kita jangan malas untuk berlatih. Semoga bermanfaat
Rumus Perkalian Aljabar dan Pembagian Aljabar Matematika
Rumus Perkalian Aljabar – Rumus Perkalian aljabar dan pembagian aljabar merupakan bentuk dari operasi hitung aljabar . Rumus perkalian aljabar prinsipnya sama halnya dengan perkalian dalam operasi hitung perkalian bilangan bulat dan begitu juga pembagian aljabar sama halnya dengan pembagian dalam bentuk bilangan bulat . Setelah kita tahu bagaimana prinsip mengalikan dan membagi bilangan , maka sekarang dalam mempelajari bentuk aljabar tidak akan sulit , karena tinggal mengaplikasikannya dalam bentuk aljabar.
Perkalian Bentuk Aljabar
Berbeda dengan penjumlahan dan pengurangan aljabar , dalam perkalian aljabar . Yang dikalikan bukan hanya koefisiennya saja , namun semua komponennya harus dikalikan .
Dan untuk menyelesaikannya digunakan metode distributif .
Bentuk perkalian satu bilangan dengan aljabar suku dua
a ( bn) = abn { suku satu }
a ( bn + c ) = abn + ac
a ( n + c ) = an + ac
bn ( n + c ) = bn2 + bcn
Keterangan :
a= sebuah bilangan
n = variabel
b = koefisien
c = konstanta
Bentuk perkalian satu bilangan dengan aljabar suku tiga :
an ( n2 + n – b ) = an3 + a n2 -b
Untuk lebih memahami tentang penjelasan diatas , perhatikan contoh soal di bawah ini :
a. Tentukan hasil perkalian dari bentuk aljabar berikut :
- 2x ( 3x + 4 y )
- 3y ( 2x + 6y )
- 4y ( 2x + 3y )
- x ( x2 – x + 1 )
- 4x ( x2 + 2 + 8 )
- 2 ( 3x + 4 ) + 6x ( x +2 )
- -4 ( x + 6 ) – 2 ( 4x – 6 )
- 6x ( 2x – 3y )
- 6 ( x2 + 2 + 1 )
- 2 ( 6x )
Jawab :
1. 2x ( 3x + 4 y ) = 6 x2 + 8xy
2. 3y ( 2x + 6y ) = 6xy + 18y2
3. 4y ( 2x + 3y ) = 8xy + 12 y2
4. x ( x2 – x + 1 ) = x3 – x2 + x
5. 4x ( x2 + 2 + 8 ) = 4 x3 + 8x + 32x
6. 2 ( 3x + 4 ) + 6x ( x +2 )
= 6x + 8 + 6x2 + 12x
= 6x2 + 6x + 12 x + 8
= 6x2 + 18x + 8
7. -4 ( x + 6 ) – 2 ( 4x – 6 )
= -4x – 24 – 8x + 12
= -12x – 12
8. 6x ( 2x – 3y ) = 12x2 – 18xy
9. 6 ( x2 + 2 + 1 ) = 6 x2 + 12 + 6
10. 2 ( 6x ) = 12x
b. Sebuah tanah yang berbentuk segi panjang memiliki lebar ( n+ 2 ) dan panjangnya ( 6n +2 ) ,maka hitunglah Luas tanah tersebut dan panjang serta lebar apabila variabel n = 2 !
Penyelesaian :
Diketahui :
p = 6n +2
l = n + 2
Ditanya :
1.Luas tanah
2. P dan l , jika n = 2
Jawab :
- L tanah = p x l
= ( 6n + 2 ) x ( n+ 2 )
= 6n x n + 6n x 2 + 2 x n + 2 x 2
= 6n2 + 12n + 2n + 4
= 6n2 + 14n + 4
Jadi , Luas tanah tersebut dalam bentuk aljabar = 6n2 + 14n + 4
atau apabila n= 2
Luas = 6n2 + 14n + 4
=6( 22 ) + 14(2) + 4
= ( 6 x 4 ) + 28 + 4
= 24 + 28 + 4
= 56
2. p = 6n +2 = 6(2) + 2 = 14
l = n + 2 = 2 + 2 = 4
Jadi , panjang nya adalah 14 dan lebarnya adalah 4
Pembagian Bentuk Aljabar
Operasi hitung dalam pembagian bentuk aljabar , yaitu sama halnya dengan pembagian bentuk bilangan bulat . Dalam bentuk bilangan bulat , untuk menyelesaikan suatu permasalahan pembagian bentuk aljbar maka langkah pertama harus mengetahui faktor persekutuan dari bentuk aljabar tersebut .
Bentuk pembagian aljabar :
an : a = an/a
= n
keterangan :
Dalam pembagian bentuk aljabar , langkah pertama yaitu merubah menjadi bentuk pecahan dimana penyebutnya adalah pembaginya .
Setelah mengubah menjadi bentuk pecahan maka selanjutnya adalah menentukan faktor persekutuan dari kedua bentuk aljabar tersebut .
Untuk memudahkan dalam mempelajari operasi hitung dalam pembagian bentuk aljabar , perhatikan contoh soal dibawah ini :
a. Tentukan hasil pembagian dari bentuk – bentuk aljabar berikut :
- 2x : 2
- 24x2 y + 12 xy2 : 4xy
- 10r : 2r
- ( 8p3 + 10p2 – 12 p ) : ( -2p )
Jawab :
1.) 2x : 2 = 2x / 2
= x
2.) 24x2 y + 12 xy2 : 4xy
Cara 1
24x2 y + 12 xy2 / 4xy
= 24x2 y / 4xy + 12xy2 / 4xy
= 6x + 3y
Cara 2
24x2 y + 12 xy2 / 4xy >> faktor persekutuannya adalah 4xy
= 4xy ( 6x + 3y ) / 4xy
= 4xy ( 6x + 3y ) / 4xy
= 6x + 3y
3.) 10r : 2r = 10r / 2r
= 5
4.) ( 8p3 + 10p2 – 12 p ) : ( -2p )
= ( 8p3 + 10p2 – 12 p ) / ( -2p )
= 8p3 + 10p2 – 12 p / -2p
= -4p2 – 5p + 6
Demikian penjelasan mengenai Rumus Perkalian Aljabar dan Pembagian Aljabar . Pada dasarnya , tidak ada masalah yang sulit . Kunci dari permasalahan matematika yaitu karena kita malas untuk memahaminya . Semakin banyak kita berlatih untuk menyelesaikan suatu soal matematik , maka semakin banyak pula kesulitan yang akan terpecahkan . Kunci dari perkalian aljabar adalah kalikan semua suku – suku yang terdapat dalam bentuk aljabar . Sedangkan kunci dari pembagian aljabar adalah membagikan antar suku dengan faktor persekutunya . Semoga bermanfaat ,

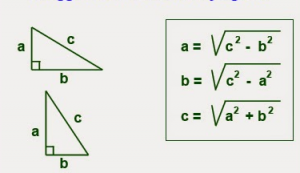

0 Response to "√Dalil Pythagoras Dalam Ilmu Matematika Lengkap Kuncinya"
Posting Komentar