√Rumus Bangun Ruang Sisi Lengkung Dalam Matematika Lengkap Kuncinya

Rumus Bangun Ruang Sisi LengkungDalam Matematika

Rumus Bangun Ruang Sisi Lengkung | Taukah anda apa yang dimaksud dengan bangun ruang sisi lengkung?dan apa sajakah yang termasuk dalam bangun ruang sisi lengkung? Dan bagaimana rumus – rumus dalam bangun sisi lengkung?Mari kita pelajari bersama.

Pengertian

Bangun ruang sisi lengkung adalah bangun ruang yang memiliki selimut dan memiliki bagian – bagian yang berupa lengkungan.

Yang termasuk dalam bangunruang sisi lengkung adalah :

1.Tabug

2.kerucut

3.Bola

Simbol – simbol yang harus di ketahui ,antara lain :

La = Luas alas

t = Tinggi

r = jari – jari lingkaran

π = terdiri dari  22/7 dan 3,14

S = garis lukis

Rumus Bangun Ruang sisi Lengkung

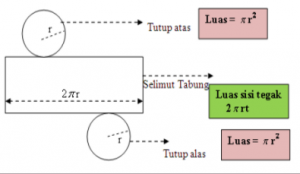
1. Tabung

Tabung dianggap sebagai prisma segi takterhingga beraturan dan merupakan bangun ruang yang terdiri atas dua bidang lingkaran yang terletak di atas dan di bawah yang besarnya sama yang dihubungkan oleh dua garis lurus yang sejajar.

Perhatikan gambar dibawah ini:

Jaring – jaring tabung :

Maka rumus yang berlaku untuk bangun ruang ini adalah :

1. Luas alas   = πr²
2. Luas tabung tertutup / Permukaan

                                  = ( ka x t ) + ( 2 x La )

                                  =  ( 2rt ) + ( 2 )

                                   =   2 ( t + r )

3. Luas tabung tanpa tutup

                    = ( ka x t ) + La

                    = 2rt +

                    = r ( 2t + r )

4. Volume tabung

           = La x t

           =  πr²t

5. Luas selimut tabung

 = ka x t

 = 2 πrt

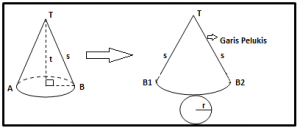
2. Kerucut

Kerucut merupakan bangun ruang sisi lengkung yang dianggap sebagai limas yang alasnya lingkaran dan memiliki garis lukis yang mengelilingi dan membentuk titik puncak.

Coba pahami gambar di bawah ini :

Dari gambar di atas maka , diketahui rumus – rumus sebagai berikut :

Volume kerucut  = 1/3 x La x t

                                   =   1/3   x   πr² x t

                                     =1/3  πr²  t

Luas selimut kerucut = 2πr / 2πs x πs2

                                           = πrs

Luas sisi kerucut = πrs +  πr²

                              = π r ( s + r )

Hubungan s, r , dan t pada kerucut :

s2 = r2 + t2

t2 = s2 – r2

r2 = s2 – t2

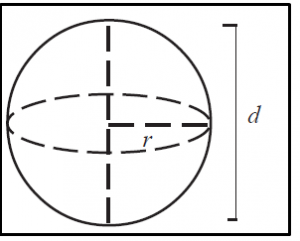
3. BOLA

Bola merupakan bangun ruang sisi lengkung yang memiliki titik pusat dan dianggap sebagai kumpulan kerucut yang terdiri dari jari – jari yang sama.

Perhatikan gambar bangun ruang di bawah ini :

Dari gambar bangun ruang di atas ,dapat di dapatkan rumus – rumus sebagai berikut :

Luas Bola = 4 πr²

Luas  bola benda berongga = 2πr²

Luas  bola benda padat / pejal = 3πr²

Volume bola

=  1/3 La x t

= 1/3 x 4πr²x r

=4/3 πr3

jari – jari ( r ) 

Utuk lebih jelasnya , maka perhatika contoh – contoh berikut .

Contoh soal

1. Diketahui suatu tabung memiliki tinggi 20 cm ,dan jari – jarinya 28 cm. Berapakah volume tabung tersebut ?

Penyelesaian :

Diketahui : t = 20   ,  r = 28

Ditanyakan : V = ….????

Jawab :

V = πr²t

   =  22/7 x 282  x 20

   = 49280  cm3

 Jadi, volume tabung tersebut adalah 49280 cm3

2. Diketahui luas suatu selimut tabung 616 cm2 , dan tingginya 7 cm. Berapakah volume tabung tersebut?

Penyelesaian :

Diketahui : Luas selimut = 616

                   t = 7

Ditanya : V = …..?????

Jawab :

V = πr²t

Karena r belum di ketahui maka langkah pertama kita cari r terlebih dahulu yaitu dengan cara subsitusi dan perkalian silang ,seperti di bawah ini :

Luas selimut =2πrt

616              = 2 x22/7  x r x 7

616 x 7      = 2 x 22 x 7 x r

4312         =308  r

r                   =  14

Setelah r di ketahui maka kita tinggal memasukan dalam rumus volume

V = πr²t

    =  22/7 x 142 x 7

    =22/7 x 196 x 7

    = 4312 cm3

Jadi volume tabung tersebut adalah 4312 cm3

3. Diketahui kerucut dengan jari – jari 5 cm dan tinggi 12 cm ,berapakah luas selimut,luas permukaan dan volume kerucut tersebut ?

Penyelesaian :

Diketahui : r = 5  , t = 12

Ditanta : a. Luas selimut = …???

1. Luas permukaan = ….???
2. volume = ….???

Jawab:

Langkah pertama yaitu mencari bagian yang belum diketahui,apakah yang belum di ketahui mari kita lihat dari rumus – rumus yang ditanyakan .

Lselimut = πrs

Lpermukaan = π r ( s + r )

Volume =  1/3  πr²  t

Jadi yang di cari pertama kali adalah s = …???????

S2 = r2 + t2

    = 52 + 122

    = 25 + 144

    = 169

S  =√169

     = 13

1. Luas selimut =  πrs

                                =3,14 x 5 x 13

                                 = 204,1 cm2

1. Luas Permukaan =  π r ( s + r )

                             = 3,14 x 5 ( 13 + 5 )

                              = 15,7 x 18

                              = 282,6 cm2

1. Volume =  1/3  πr²  t

              = 1/3  x 3,14 x 5 x 5 x 12

              = 314 cm3

4. Suatu bola memiliki volume 381,51 cm3, hitunglah jari – jari bola tersebut !

Penyelesaian :

Diketahui : v bola = 381,51

Ditanya : r = …???

Jawab

V             =  4/3 πr3

  381,51  =4/3   x 3,14 x r3

     r3          = ( 381,51 x 3 ) : ( 4 x 3,14 )

                      =91,125

     r          = 4,5 cm

5. Perhatikan gambar dibawah ini ,

        Apabila jari jarinya 7 cm dan tingginya 24, maka hitunglah:

1. Volumenya
2. Apabila 1cm3 beratnya 12 gr maka ,hitunglah berat benda tersebut !
3. Luas permukaan benda tersebut

Penyelesaian :

Diketahui : r = 7  , t = 24

Jawab :

1. Volume benda = V kerucut + V setengah bola

                       = 1/3  πr²  t  +  2/3 πr3

                   =1/3 x 22/7  x 7 x 7 x 24 +  2/3   x 22/7   x 7 x 7 x 7

                  = 1232 + 718,67

                  = 1950,67 cm3

2. Berat benda = 1950,67 x 12 gr

                     = 23408,04 gr

                     = 23,40804 kg

3. s = √7²  + 24²

       =  √49 + 576

       =√ 625

       =  25

Lselimut = π rs

                =22/7  x  7  x 25

               = 550 cm2

L setengah bola berongga = 2πr²

                                                              = 2 x  22/7 x 7 x 7

                                                = 308 cm2

Lpermukaan benda = Lsel + Lsetbola

                               = 550 + 308

                               = 858 cm2

Demikian penjelasan mengenai Macam – macam dan Rumus Bangun Ruang sisi lengkung . Dalam menyelesaikan soal bangun ruang sisi lengkung itu mudah , cuma kita harus faham dengan rumus – ruusnya , jangan sampai tertukar antara bangun ruang yang satu dengan yang lainnya . Karena rumusnya hampir sama . Semoga bermanfaat

Rumus Perpangkatan Aljabar Matematika

Rumus Perpangkatan Aljabar – Rumus perpangkatan aljabar sama prinsipnya dengan perpangkatan pada bilangan bulat . Perpangkatan yaitu perkalian yang diulang dengan suatu  bilangan yang sama .

Rumus perpangkatan secara umum : 

Rumus Perpangkatan Aljabar :

( a + b )n  = ( a + b )  x ( a + b ) x  ( a + b ) , . . . x ( a + b )

Dengan ( a + b ) sebanyak n

Sebelum Mengetahui bagaimana cara untuk menyelesaikan perpangkatan bentuk aljabar , maka yang perlu diperhatikan yaitu :

• abn   berbeda dengan (ab )n 

Dalam bentuk abn  maka yang dipangkatkan n  hanya b nya saja , namun pada bentuk (ab )n   maka yang dipangkatkan n semuanya , yaitu (ab)

Contoh :

( 2a )2    = ( 2a )( 2a ) = 4a2

Sedangkan

2a2     = 2 x a x a = 2a2

• ( -ab )n  berbeda dengan  – (ab )n

Dalam bentuk ( -ab )n  ,maka yang dipangkatkan n adalah   ( -ab ) . Sedangkan dalam bentuk – (ab )n  yang dipangkatkan n adalah ab

Cara menyelesaikan Perpangkatan Aljabar 

Apabila suatu bilangan aljabar berpangkat 2 maka masih mudah dalam mengerjakannya namun bagaimana cara untuk mengerjakan atau menyelesaikan perpangkatan aljabar yag pangkatnya lebih dari 2 ?

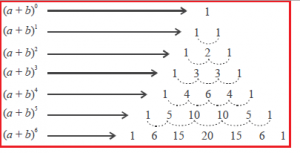
Sebelum mengetahui bagaimana cara untuk menyelesaikan perpangkatan aljabar yang lebih dari dua , kita harus mengetahui terlebih dahulu mengenai segitiga pascal . Mengapa demikian ? Karena dalam penyelesaian perpangkatan aljabar segitiga pascal sangat membantunya .

Perhatikan segitiga pascal berikut ini :

Cara penggunaan segitiga pascal dalam penyelesaian perpangkatan aljabar:

( a + b )0  = 1

( a + b )1  = a + b

( a + b )2  = a2  +  2ab  + b2

( a + b )3  = a3  +  3a2b +  3ab2  + b3

( a + b )4  = a4  +  4a3b +  6a2b2  + 4ab3 + b4

( a + b )5 =  a5  +  5a4b +  10a3 b2  + 10a2b3 + 5ab4 + b5

Contoh Soal 

A . Tentukan hasil perpangkatan bilangan tersebut !

1. (-2a )2 
2. – ( 3b )3
3. ( 2xy )2

Penyelesaian

1. (-2a )2    =  (-2a)  x  (-2a )

                         = 4a2

2. – ( 3b )3    =   – { (3b) ( 3b ) ( 3b ) }

                      = – 27b3

B. Berapakah hasil perpangkatan bentuk aljabar berikut ?

1. ( -2x )2 
2. ( x + 2y)2 
3. ( x + 2 )3
4. ( 3x +  6 ) 3
5. ( -3a + 2b)2
6. (7x -8 ) 3
7. ( 3a – 2 )4 
8. ( 2x – 2)2

Penyelesaian :

1. ( -2x )2 = ( -2x ) x ( -2x )

                        = 4x²

2. Rumus ( a + b )2 = a2  +  2ab  + b2 

maka :

( x + 2y)2   =  x2  +  2(2xy)  + 2xy2

                   =  x2  +  4xy  + 2xy2

3. Rumus ( a + b )3 = a3  +  3a2b +  3ab2 + b3

maka :

( x + 2 )3  =  x3  +  3x22 +  3×22  + 23

                      = x3 + 6x2 + 12x + 8

4. Rumus ( a + b )3 = a3  +  3a2b +  3ab2 + b3

maka :

( 3x + 6 ) 3 =  3x3  +  3(3x)26 +  3(3x)62  + 63

                   =  3x3  + ( 3 . 3x . 3x . 6 )+ 3(3x)36 + 216

                  = 3x3  + (3 . 9x2  . 6 ) + 324x + 216

                 =  3x3  + 162 + 324x + 216

5. Rumus : ( a + b )2 = a2  +  2ab  + b2 

Maka :

( -3a + 2b)2  = -3a2  +  2(-3a)2b  + 2b2 

                      =  -3a2 + (-12ab ) + (2b . 2b )

                     =  -3a2  -12ab  + 4b2 

6. Rumus : ( a + b )3 = a3  +  3a2b +  3ab2 + b3

Maka :

(7x -8 ) 3 = a3  +  3a2b +  3ab2  + b3

                = 7x3  + 3(7x)2(-8) + ( -8 )3

               = 7x3  + 1176x2 – 512

Tips dalam menyelesaikan perpangkatan aljabar :

a. Memahami bentuk perpangkatan .

b. Memahami pola dalam segitiga pascal , ( a+b )n

c. Mensubstitusikan  dari bentuk perpangkatan aljabar kedalam pola  segitiga pascal .

Demikian penjelasan mengenai rumus perpangkatan bentuk aljabar . Kunci dari rumus perpangkatan bentuk aljabar yaitu memahami pola segitiga pascal dan memahami tanda – tanda bilangan . Jangan sampai salah dalam memangkatkan . Semoga bermanfaat

Cara Menghitung Rumus Pemfaktoran Aljabar Matematika

Rumus Pemfaktoran Aljabar – Rumus pemfaktoran aljabar yaitu sebuah rumus untuk menyatakan sebuah bentuk persamaan aljabar menjadi sebuah bentuk perkalian aljabar atau faktorisasinya . Dalam pembahasan sebelumnya , kita telah mengenal istilah faktorisasi aljabar . Faktor dari sebuah bilangan yaitu bilangan  pembagi habis suatu bilangan tersebut . Contohnya bentuk aljabar ab = a x b , faktorisasinya = a dan b . bentuk aljabar a(x + y ) maka faktorisasinya a dan (x+y ) . Untuk memahami lebih dalam mengenai rumus pemfaktoran , perhatikan penjelasan dibawah ini .

Metode Pemfaktoran Aljabar

1. Sifat Distributif 

Sifat distributif dapat digunakan untuk memfaktorkan bentuk aljabar dengan mencari FPB dari bentuk alhabar tersebut . Persamaan yang dapat diselesaikan menggunakan sifat distributif yaitu bentuk aljabar :

Contoh soal :

Faktorkan bentuk – bentuk aljabar berikut ini :

a.  3x2 y + 6xy2

b. 15pq + pq2 r

c.  2a2  + 4a2 y

d. 2a2  + 8a2 b

e.   3x2 y + 9xy2

Penyelesaian :

Untuk menyelesaikan soal di atas maka langkah pertama yaitu mencari Fpb dari bentuk aljabar tersebut .

a.  3x2 y + 6xy2

FPB dari  3x2 y + 6xy2  adalah 3xy

jadi bentuk pemfaktorannya :   3x2 y + 6xy2  =  3xy ( x + 2y )

b.  15pq + pq2 r

FPB dari  15pq + pq2 r  adalah pq

jadi bentuk pemfaktorannya :  15pq + pq2 r = pq ( 15 + qr )

c.  2a2  + 4a2 y

FPB dari 2a2  + 4a2 y = 2a

jadi , bentuk pemfaktorannya :  2a2  + 4a2 y = 2a ( a + 2ay )

d. 2a2  + 8a2 b

FPB dari 2a2  + 8a2 b = 2a

jadi , bentuk pemfaktorannya : 2a2  + 8a2 b = 2a ( a + 4ab )

e.   3x2 y + 9xy2

FPB dari 3x2 y + 9xy2   = 3xy

jadi , bentuk pemfaktorannya : 3xy ( x + 3y )

2. Pemfaktoran Dalam Bentuk selisih kuadrat 

Cotoh soal :

Faktorkan bentuk aljabar berikut ini :

a.  x2 – 2 2

b. 42 − x2 

c. 5 2 − x2 

d. 4x2 − 16

e. 9x8 − 4y4

Penyelesaian :

a.   x2 – 2 2  = ( x+ 2 ) ( x – 2 )

b.  42 − x2   = ( 4 + x ) ( 4 – x )

c. 5 2 − x2    =  ( 5 + x ) ( 5 – x )

d.  4x2 − 16

= (2x)2  – ( 4 ) 2

= ( 2x + 4 ) ( 2x – 4 )

e. 9x8 − 4y4

= (3x4 )2  – ( 2y2 )2

= ( 3x4 +  2y2  ) ( 3x4 –  2y2  )

3. Pemfaktoran Aljabar Dalam Bentuk Kuadrat yang sempurna 

atau

Contoh Soal :

a. a2 + 10a + 25

b. x2 − 16 x + 64

c. 16b2 − 20bc + 25c2

d. p2 – 10p + 25

e. 16a2 + 16a + 4

Penyelesaian :

a.  a2 + 10a + 25 = ( a + 5 ) ( a + 5 )

b.  x2 − 16 x + 64 = ( x – 8 ) ( x – 8 )

c. 16b2 − 40bc + 25c2 

= ( 4b -5c ) ( 4b – 5c )

d.  p2 – 10p + 25 = ( p – 5 ) ( p – 5 )

e.  16a2 + 16a + 4

= ( 4a + 2 ) ( 4a + 2 )

4. Pemfaktoran Aljabar Dalam Bentuk  ax2  + bx + c = 0 , dan a = 0

Contoh soal :

a. a 2 + 7a + 12

b. p2 + 6p +8
c. n2 + 9n + 14

d. q2 + 9q + 18

Penyelesaian :

Langkah pertama , yaitu menentukan dua angka yang apabila di jumlah sama dengan angka tengah dan apabila di kali sama dengan huruf yang ke tiga .

a.  a 2 + 7a + 12 = ( a + 4 ) ( a + 3 )

karena  angka 4 dan 3 diatas apabila  4 + 3 = 7 dan 4 x 3 = 12

b.  p2 + 6p + 8 = ( p + 2 ) ( p + 4 )

karena  angka 2 dan 4 diatas apabila 2 + 4 = 6 dan apabila 2 x 4 = 8

c. n2 + 9n + 14 = ( n + 2 ) ( n + 7 )

karena  angka 3 dan 7 diatas apabila 2 + 7 = 9  , dan 2 x 7 = 14

d. q2 + 9q + 18 = ( q + 3 ) ( q + 6 )

karena angka 3 dan 6 diatas apabila 3 + 6 = 9 dan 3 x 6 = 18

5. Pemfaktoran Aljabar Dalam Bentuk  ax2  + bx + c = 0 , dan a ≠ 0

 ax2  + bx + c = 0

Contoh soal 

a. 5x2  + 13 – 6  = 0

Pembahasan :

5x2  + 13 – 6  = 0

a x c = m x n , m + n = b

jadi ,  angka yang cocok adalah  15 dan -2 , karena  5 x -6 = 15 x – 2 dan 15 + (-2 ) = 13 maka

          5x2  + 13 – 6

< = > 5x2  + 15x -2 x -6

< = > 5x ( x + 3 ) – 2 ( x + 3 )

< = >( 5x – 2 ) ( x + 3 )

b. 2x2  + 11x – 6

Pembahasan :

2x2  + 11x – 6

a x c = m x n , m + n = b

jadi , angka yang cocok adalah 12 dan – 1 , karena 2 x -6 = 12  x -1 dan 12 + ( -1 ) = 11 maka

2x2  + 11x – 6

<=> 2x2  + 12x – x – 6

<=> 2x ( x + 6 ) -( x + 6 )

<=> ( 2x -1 ) ( x + 6 )

Demikian penjelasan mengenai Cara untuk menghitung Rumus Pemfaktoran Bentuk aljabar secara lengkap . Dan telah dijelaskan beserta dengan contohnya . Inti dari pemfaktoran bentuk aljabar yaitu harus memahami FPB dari suatu bilangan . Karena jika tidak mengetahui maka akan sulit untuk mempelajarinya . Selain itu juga untuk memudahkan dalam menyelesaikan soal pemfaktoran aljabar langkah pertama harus memahami bentuk dari persamaan tersebut . Bentuk dari persamaan aljabar telah dijelaskan di atas . Selalu semangat untuk belajar , karena ilmu matematika adalah ilmu yang sangat mudah untuk dipelajari apabila yang mempelajari itu bersungguh – sungguh .

Tweet

Subscribe to receive free email updates: