Rumus Penjumlahan Aljabar dan Pengurangan Aljabar
Rumus Penjumlahan Aljabar – Rumus penjumlahan aljabar dan pengurangan aljabar sama halnya dengan penjumlahan ataupun pengurangan bentuk bilangan bulat . Aljabar merupakan salah satu cabang aritmatika dalam ilmu matematika yang ditemukan oleh ilmuwan arab yang bernama ” Abu Abdullah Muhamad ibnu Musa Al Khawarizi ” . Aljabar memiliki arti suatu cara untuk menyelesaikan atau memecahkan suatu masalah .
Macam – Macam bentuk aljabar
Aljabar di bagi dalam 5 macam , yaitu :
1. Aljabar elementer ( aljabar dasar ) , yaitu bentuk aljabar untuk menyelesaikan bilangan riil yang menggunakan peubah untuk menandakan variabel dan konstanta.
2. Aljabar Linier
3. Aljabar Abstrak
4. Aljabar Universal
5. Aljabar komputer
Istilah – istilah yang perlu di fahami dalam bentuk aljabar
Istilah – istilah ini merupakan unsur – unsur yang terdapat dalam bentuk aljabar , unsur – unsur tersebut adalah :
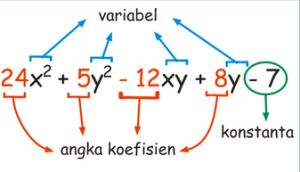
1. Variabel disebut juga dengan peubah , yang memiliki pengertian lambang pengganti bilangan yang belum di ketahui . Contoh variabel : x , y , a , b , xy
2. Koefisien yaitu angka yang terdapat di depan variabel .
contoh : x+3 = koefisiennya adalah 1 , 3x+5 = koefisiennya adalah 3
3. Konstanta ,yaitu suku dari suatu bentuk aljabar yang berdiri sendiri
contoh : 4x + 5y + 6 , maka konstanta dari bentuk aljabar tersebut adalah 6
4. Suku , yaitu nilai yang menyusun suatu bentuk aljabar yang berupa variabel , koefisien ataupun konstanta .
macam – macam suku :
1. Menurut jenisnya :
- Suku sejenis , yaitu bentuk aljabar yang variabel dan pangkatnya sama contoh : 3x dan x , 3xy dan xy
- suku tak sejenis , yaitu bentuk aljabar yang variabel dan pangkatnya tak sama .contoh : 4x dan 4y , 2xy dan 3xy2 , 2xy dan x
2. Menurut jumlah sukunya :
- suku satu , yaitu bentuk aljabar yang berdiri sendiri yang tidak dihubungkan oleh operasi penjumlahan ataupun selisih . contoh x , 2x
- suku dua , yaitu bentuk aljabar yang dihubungkan oleh operasi penjumlahan ataupun selisih . contoh: x+y , 3x- y
- suku tiga , yaitu bentuk aljabar yang dihibungkan oleh 2 operasi penjumlahan ataupun selisih . contoh : x+y+7, 2x+2xy+2
Operasi bentuk aljabar
operasi hitung dalam aljabar , sama halnya dengan operasi hitung bilangan bulat yaitu meliputi :
1. Penjumlahan bentuk aljabar
2. Pengurangan bentuk aljabar
3. Perkalian bentukaljabar
4. Pembagian bentuk aljabar
5. Perpangkatan bentuk aljabar
Dalam kesempatan kali ini , kita akan mempelajari penjumlahan dan pengurangan aljabar .
Penjumlahan dan Pengurangan Bentuk Aljabar
Bentuk aljabar yang dapat dijumlahkan atau dikurangkan yaitu hanya pada bentuk aljabar yang memiliki suku yang sama . Dalam penjumlahan dan pengurangan yang dijumlah ataupun dikurangkan adalah koefisiennya dalam suku yang sama .
Penjumlahan Bentuk Aljabar
an + bn = ( a + b )n
Pengurangan Bentuk Aljabar
an – bn= ( a – b ) n
Keterangan :
a dan b = koefisien
n = Variabel
Contoh soal
1. Tentukan koefisien dari bentuk – bentuk aljabar berikut :
a. 2x2 + x – 1
b. 3x2 +- 2x + 1
c. x2 + 5x – 6
d. ax3 + bx2 + cx + d
Jawab :
a. koefisien x2 = 2 dan x = 1
b. koefisien x2 = 3 dan x = 2
c. koefisien x2 = 1 dan x = 5
d. koefisien x3 = a , x2 = b dan x = c
2. Sederhanakan bentuk aljabar berikut :
a. 3x2 – 4 x2 + 7x – 2 x + 1
b. 4x2 – 2y + 1 – 5x2 + x + y
c. 4 ( 2x2 – y ) + 3 ( x2 + y )
Jawab :
a. 3x2 – 4 x2 + 7x – 2 x + 1
= ( 3 – 4 ) x2 + ( 7 – 2 )x + 1
= -1 x2 + 5x + 1
b. 4x2 – 2y + 1 – 5x2 + x + y
= (4 – 5 )x2 – ( 2 + 1 ) y + 1 + x
= -1x2 – 3y +1 + x
c. 4 ( 2x2 – y ) + 3 ( x2 + y )
= ( 4 + 3 ) + ( 2 + 1 ) x2 + ( -y + y )
= 7 + 3x2 – y + y
3. Tentukan suku – suku sejenis dari pasangan berikut :
a. x2 + 2x2 – 1 dengan 3x2 + x +xy
b. 2x2 + x dengan –x2 +2
c. -2x +5 dengan 5x2 -2
d. x3 – x2 dengan 4x2 + x
Jawab :
a. x2 + 2x – 1 dengan 3x2 + x +xy
suku – suku yang sejenis adalah : x2 dan 3x2 , 2x dan x
b. 2x2 + x dengan –x2 +2
suku – suku yang sejenis adalah : 2x2 dan –x2
c. -2x +5 dengan 5x2 -2
suku – suku yang sejenis adalah : s dan -2
d. x3 – x2 dengan 4x2 + x
suku – suku yang sejenis adalah : – x2 dan 4x2
4. Tentukan penjumlahan dari bentuk aljabar berikut :
a. 4x + x
b. 5xy + 6xy
c. 3xy + 3 + 4xy +1
d. ( 3x + 4xy + 2 ) + ( 3 + 4x + 2xy )
Jawab :
a. 4x + x = 5x
b. 5xy + 6xy = 11xy
c. 3xy + 3 + 4xy +1
= ( 3 + 4 ) xy + ( 3 + 1 )
= 7xy + 4
d. ( 3x + 4xy + 2 ) + ( 3 + 4x + 2xy )
= 3x + 4xy + 2 + 3 + 4x + 2xy
= ( 3x + 4x ) + ( 4xy + 2xy ) + ( 2 + 3 )
= 7x + 6xy + 5
5. Tentukan hasil pengurangan dari bentuk aljabar berikut :
a. 5xy – xy
b. 3y – 5y
c. -x – 4x
Jawab :
a. 5xy – xy = 4 xy
b. 3y – 5y = -2y
c. -x -4x = -5x
6. Tentukan hasil dari penjumlahan dan pengurangan dari bentuk aljabar berikut :
a. -2x2 + 5x2
b. ( -5 x3 + 4x2 -7 ) + ( x2 -x + 4 )
c. ( 3p3 – 2aq2 + 5 ) – ( p2 – aq2 -10 )
d. 3x2 – 4x2 + 7x – 2x +1
Jawab :
a. -2x2 + 5x2
= ( -2 + 5 ) x2
= 3 x2
b. ( -5 x3 + 4x2 -7 ) + ( x2 -x + 4 )
= -5 x3+ ( 4 + 1 )x2 – x + ( -7 + 4 )
= -5 x3 + 5x2 – x -3
c. ( 3p3 – 2aq2 + 5 ) – ( p2 – aq2 -10 )
= 3p3 – p2 – ( 2 – 1 ) aq2 + ( 5 – 10 )
= 3p3 – p2 – aq2 -5
d. 3x2 – 4x2 + 7x – 2x +1
= ( 3 – 4 ) x2 + ( 7 – 2 ) x + 1
= -1 x2 – 5x + 1
Demikian penjelasan mengenai rumus penjumlahan dan pengurangan bentuk aljabar . Kunci untuk menyelesaikan sebuah permasalahan dari bentuk aljabar khususnya penjumlahan dan pengurangan yaitu memahami suku – suku yang sejenis dan pangkatnya sama . Setelah kita memahami itu semua , maka pemahaman tentang penjumlahan dan pengurangan dapat kita langsung kita aplikasikan ke dalamnya . Sesungguhnya sesuatu yang terlihat sulit , apabila kita serius dalam berlatih dan berusaha memahaminya itu semua dapat berubah menjadi hal yang sangat mudah .
Rumus Perkalian Matriks dan Perkalian Skalar Matriks
Rumus Perkalian Matriks – Pengertian Rumus Perkalian Matriks ialah nilai Matriks yg dapat dikalikan dg cara setiap baris yg dikalikan dg tiap kolom dg jumlah pd baris yg sama. Sedangkan untuk Rumus Matematika Perkalian Matriks ini sebenarnya merupakan suatu turunan dari Operasi Dasar Matriks karena Macam Matriks Matematika menurut Operasi Dasar Matriks nya dibagi antara lain Rumus Penjumlahan Matriks, Rumus Pengurangan Matriks, Rumus Perkalian Skalar matriks dan Rumus Mencari Perkalian Matriks.
Sedangkan untuk Jenis Rumus Matriks dibagi antara lain Rumus Matematika Matriks Baris ialah Matriks yg mempunyai satu baris saja, Rumus Menghitung Matriks Kolom ialah Matriks yg hanya mempunyai satu kolom, Rumus Mencari Matriks Nol ialah Matriks Matematika yg semua komponenya bernilai bilangan Nol, Matriks Persegi ialah Matriks yg memiliki baris dan kolom yg sama banyaknya dan Rumus Matriks Matematika Segitiga Alas, Matriks Diagonal, Matriks Segitiga bawah serta Matriks Skalar dan Matriks Identitas.
Dari semua Jenis dan Macam Matriks Matematika diatas, disini kami akan menjelaskan dan memberikan penjelasan kepada anda tentang Rumus Perkalian Matriks dan Rumus Perkalian Skalar Matriks Matematika secara lengkap dan detail karena disini kami jg akan memberikan Contoh Soal Perkalian Matriks sehingga bisa memudahkan anda dlm memahami Rumus Menghitung Perkalian Matriks yg sudah kami jelaskan.
Cara Menghitung Rumus Perkalian Matriks dan Rumus Perkalian Skalar Matriks
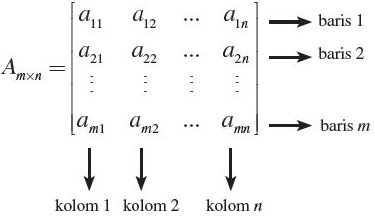
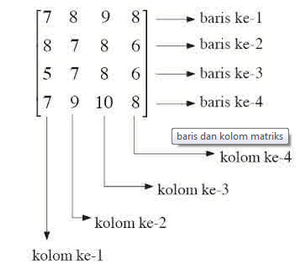
Jika anda melihat gambar diatas maka melihat adanya kolom dan baris yg digunakan untuk menentukan dan menghitung nilai Matriks. Kolom dan Garis memang sangat dibutuhkan didalam menghitung nilai Matriks karena Pengertian Matriks Matematika sendiri yaitu suatu bilangan yg tersusun dlm bentuk menyerupai persegi panjang dg tanda kurung () atau dg tanda kurung siku [] atau disusun didalam kolom dan baris yg mempunyai ukuran nilai dan dlm hal ini disebut dg Ordo Matriks.
Rumus Perkalian Matriks Matematika
Operasi Cara Mencari Rumus Perkalian Matriks Matematika mempunyai Metode Rumus Menghitung Matriks yg sangat berbeda dg Operasi menghitung nilai penjumlahan atau pengurangan Matriks, Metode yg diterapkan didalam Rumus Menghitung Perkalian Matriks ialah dg memasangkan baris pd matriks pertama dg kolom pd matriks kedua tetapi kedua nilai Matriks ini bisa dikalian jika banyak kolom pd matriks pertama mempunyai nilai yg sama dg banyak baris pd matriks kedua dan hasil perkalian matriks akan mempunyai baris yg sama banyak dg baris matriks pertama.
Rumus Perkalian Matriks Skalar
Sedangkan untuk penjelasan dari Rumus Perkalian Skalar Matriks dilakukan dg cara konstanta yg artinya nilai matriks bisa dikalikan dg cara mengalikan setiap eleman atau komponen nilai matriks dg skalar. Misalnya nilai Matriks A dikalikan dg skalar K maka setiap eleman atau komponen Matriks A dikali dg k.
Soal Matematika Perkalian Matriks
Setelah anda melihat penjelasan dari kami dari kedua Rumus Matematika Perkalian Matriks diatas maka sudah saatnya kami memberikan contoh Soal Perkalian Matriks sehingga bisa berguna untuk memudahkan anda dlm memahami Rumus Matematika Matriks yg sudah kami jelaskan diatas.
Hanya seperti itulah penjelasan yg bisa kami berikan kepada anda semua dan semoga penjelasan Rumus Menghitung Perkalian Matriks dapat berguna dan bermanfaat bagi anda semuanya baik siswa atau siswi maupun para mahasiswa karena tujuan kami dlm penulisan ini ditujukan untuk kalian semuanya.
Rumus Penjumlahan Matriks dan Pengurangan Matriks
Rumus Penjumlahan Matriks – Pengertian Rumus Matriks Matematika jika melihat dari para ahli Matematika ialah kumpulan simbol atau ekspresi dan kumpulan bilangan – bilangan yg berbentuk menyerupai persegi panjang yg disusun atas baris dan kolom. Kemudian Bilangan – Bilangan Matriks Matematika tersebut bisa disebut pula dg elemen atau komponen bilangan Matriks dan hal ini sudah kami pernah jelaskan kepada anda didalam artikel Rumus Matematika Matriks Terlengkap.
Seperti yg pernah kami jelaskan kepada anda didalam artikel Rumus Menghitung Matriks tersebut disebutkan bahwa ada Macam – Macam Matriks didalam Operasi Dasar Matriks yg terbagi atas Rumus Penjumlahan Matriks, Rumus Pengurangan Matriks, Rumus Perkalian Skalar Matriks dan Rumus Perkalian Matriks. Sedangkan untuk Macam dan Operasi Dasar Matriks tersebut bisa dikatakan sangatlah penting semuanya karena Kumpulan Rumus Matriks itu masih sering muncul didalam soal ujian nasional atau soal ujian sekolah yg bisa menentukan lulus atau kenaikan kelas anda sebagai siswa dan siswi tingkat SMP maupun SMA.
Oleh karena itu disini kami akan memberikan penjelasan kepada anda tentang Rumus Penjumlahan Matriks dan Rumus Pengurangan Matriks secara lengkap dan detail karena dilengkapi dg Contoh Soal Matematika Penjumlahan dan Pengurangan Matriks. Namun sekali lagi kami sampaikan kepada anda bahwa Rumus Mencari Matriks digunakan untuk menyelesaikan suatu permasalahan matematika di tingkat SMA maupun SMP.
Rumus Penjumlahan Matriks dan Rumus Pengurangan Matriks Matematika
Cara Menghitung dan Mencari Rumus Matriks ialah menggunakan sistem kolom dan baris seperti gambar diatas karena Nilai suatu Matriks Matematika merupakan suatu eleman dan komponen yg sudah disusun atas baris dan kolom sehingga jika anda menghitung dan mencari Nilai Matriks dlm sebuah Soal Matematika maka anda harus susun nilai – nilai tersebut kedalam kolom dan baris.
Cara Mencari Rumus Penjumlahan Matriks
Pengertian dari Rumus Menghitung Penjumlahan Matriks ialah dua matriks yg dpt dijumlahkan ketika nilai kedua matriks matematika tersebut memiliki ordo yg sama dg nilai Matriks yg dijumlahkan. Komponen atau Eleman Matriks hasil dari penjumlahkan diperoleh dg cara menjumlahkan komponen atau eleman disetiap matriks yg seletak, sebagai contohnya bisa anda lihat dua Matriks dg Ordo 2×2 dibawah ini.
Mungkin untuk dapat mempermudahkan anda dlm memahami Rumus Mencari Penjumlahan Matriks Matematika diatas bisa anda lihat Contoh Soal Matematika Penjumlahan Matriks yg sudah kami sertakan jawabanya sekalian.
Cara Menghitung Rumus Pengurangan Matriks
Sedangkan untuk Rumus Menghitung Pengurangan Matriks dan Rumus Mencari Pengurangan Matriks sama saja seperti Pengurangan Matriks Matematika A oleh nilai Matriks B maka ditulis A – B adlh penjumlahan Matriks A dg lawan dari Matriks B yaitu -B. Jika dilihat seperti itu maka diperoleh konsep Rumus Pengurangan matriks yg sama dg Rumus Penjumlahan Matriks dan Syarat yg terdapat didlm penjumlahan matriks berlaku jg untuk pengurangan matriks. Untuk lebih membantu anda dlm memahami Rumus Menghitung Pengurangan Matriks Matematika diatas maka bisa anda lihat Contoh Soal Matematika Pengurangan Matriks dibawah ini.
Contoh Soal Pengurangan dan Penjumlahan Matriks
Walaupun diatas sudah kami berikan Contoh Soal – Soal Penjumlahan dan Pengurangan Matriks Matematika, tetapi dibawah ini kami akan memberikan Contoh Soal Matriks Matematika lainnya sehingga anda bisa lebih memahami dan mengerti akan Rumus Penjumlahan dan Pengurangan Matriks yg sudah kami berikan penjelasanya diatas.
Sebelum mengakhiri tulisan ini, kami akan memberitahukan kepada anda bahwa Rumus Penjumlahan Matriks dan Rumus Pengurangan Matriks digunakan apabila kedua nilai matriks tersebut memiliki ukuran dan tipe yg sama serta eleman atau komponen yg dijumlahkan atau dikurangkan dg posisi dan letak yg sama.

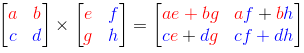
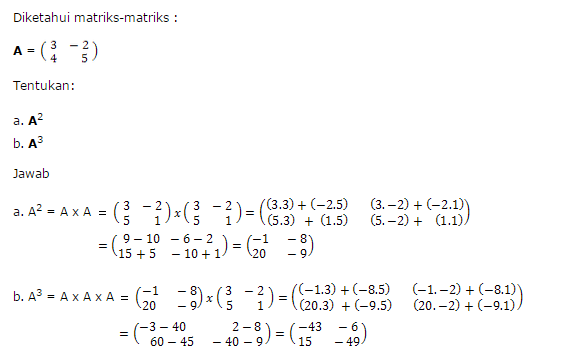
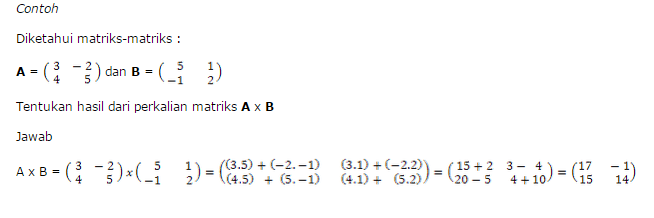



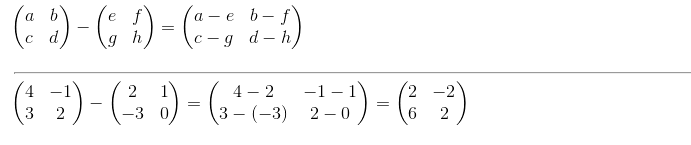

0 Response to "√Rumus Penjumlahan Aljabar Dan Pengurangan Aljabar Lengkap Kuncinya"
Posting Komentar