Operasi Hitung Pecahan Aljabar Dan Contoh Soalnya
Selain dalam bentuk bilangan biasa , dalam bentuk aljabar juga terdapat yang namanya pecahan aljabar . Bagaimanakah cara untuk menyelesaikannya ? apakah sama prinsipnya dengan pecahan biasa ? ataukah berbeda ?
Diantara kita masih banyak yang beranggapan ketika mendengar kata aljabar bayangannya pasti sulit dan pasti membosankan . Apalagi ada tambahan kata pecahan , ini bagi sebagian orang pasti sudah takut terlebih dahulu dan bayangannya bahwa bentuk hitung ini sangat sulit dan rumit .
Untuk itu , mari kita pelajari bersama bagimana cara memecahkan operasi hitung pecahan aljabar supaya mudah untuk diselesaikan dan supaya anggapan – anggapan mengenai matematika itu sulit dan membosankan dapat kita rubah menjadi matematika itu mengasyikkan .
Dan sesungguhnya apabila kita cermati secara saksama , operasi hitung bentuk biasa dengan bentuk pecahan itu sama tidak ada bedanya . Jadi ,dengan kata lain kita harus fahan terlebih dahulu mengenai operasi hitung dasar . Operasi hitung dasar yaitu penjumlahan , pengurangan , perkalian , dan pembagian . Setelah kita memahaminya , maka tinggal kita aplikasikan ke dalam bentuk yang lain atau kali ini ke dalam bentuk pecahan aljabar .
Operasi Hitung Pecahan Bentuk Aljabar
Seperti dalam pecahan bentuk biasa , dalam pecahan bentuk aljabar juga ada 4 operasi hitung yaitu :
- Penjumlahan pecahan bentuk aljabar
- Pengurangan pecahan bentuk aljabar
- Perkalian pecahan bentuk aljabar
- Pembagian pecahan bentuk aljabar
Untuk lebih jelasnya , perhatikan penjelasan di bawah ini :
1. Penjumlahan Dan Pengurangan Pecahan Bentuk Aljabar
Untuk menyelesaikan pecahan bentuk aljabar , prinsipnya sama dengan menyelesaikan penjumlahan pecahan biasa yaitu dengan cara menyamakan penyebutnya terlebih dahulu baru di jumlahkan atau dikurangkan .
Perhatikan contoh – contoh di bawah ini :
- Sederhanakan benuk pecahan aljabar berikut
Penyelesaian:
- Selesaikan bentuk pecahan aljabar berikut ini :
Penyelesaian :
Dari contoh – contoh diatas ,dapat kita simpulkan bahwa ketika akan menyelesaikan operasi hitung penjumlahan dan pengurangan kita lihat terlebih dahulu penyebutnya . Jika sama , maka langsung kita jumlahkan atau kurangkan . Namun , jika berbeda penyebutnya maka kita samakan terlebih dahulu baru kita kurangkan atau jumlahkan . Atau dengan kata lain prinsip penyelesaian operasi hitung pecahan biasa dan pecahan aljabar sama .
2. Perkalian Dan Pembagian Pecahan Bentuk Aljabar
a. Perkalian Pecahan Bentuk Aljabar
Cara untuk menyelesaiakan operasi hitung pecahan bentuk aljabar prisnsipnya sama dengan perkalian pecahan bentuk biasa . Yaitu dengan cara mengalikan pembilang dengan pembilang dan mengalikan penyebut dengan penyebut .
Rumus :
Untuk lebih jelasnya , perhatikan contoh di bawah ini :
- Sederhanakan perkalian pecahan bentuk aljabar berikut
Penyelesaian :
b. Pembagian Pecahan Bentuk Aljabar
Untuk menyelesaiakan pembagian pecahan bentuk aljabar , caranya sama dengan menyelesaikan pembagian pecahan biasa , yaitu dengan cara merubah ke bentuk perkalian dimana bilangan kedua dibalik, penyebut menjadi pembilang dan pembilang menjadi penyebut .
Rumus
Supaya lebih jelas lagi , perhatikan contoh di bawah ini :
- Sederhanakan bentuk pembagian pecahan aljabar berikut :
Penyelesaian:
3. Perpangkatan Pecahan Bentuk Aljabar
Perpangkatan yaitu perkalian perulangan bilangan dengan bilangan yang sama . Hukum ini berlaku juga dalam bentuk pecahan aljabar .
Rumus :
Untuk lebih jelasnya , perhatikan contoh berikut ini :
- Sederhanakan pecahan bentuk aljabar berikut :
Penyelesaian :
Demikian penjelasan mengenai operasi hitung pecahan bentuk aljabar . Mudah bukan ? inti dari pecahan aslinya sama yaitu ketika dijumlahkan atau dikurangkan maka penyebutnya harus sama . Dan apabila akan di bagikan maka rubah ke dalam bentuk perkalian dimana penyebut dan pembilang di bilangan ke dua di balik . Dan ketika mengalikan bentuk pecahan tinggal dikalikan penyebut dengan penyebut dan pembilang dengan pembilang . Dan ketika menyederhanakan bentuk pecahan ketika sudah tidak memiliki faktor yang sama kecuali 1 . Atau seperti yang telah di contohkan di atas .
Inti dari operasi hitung diatas adalah harus menguasai operasi hitung penjumlahan , pengurngan , perkalian ,pembagian , perpangkatan serta memahami apa itu FPB atau memahami faktorisasi dari kedua pecahan yang sedang di hadapi atau yang akan diselsesaikan .
Pengertian Dan Metode Penyelesaian SPLDV Secara Lengkap
Pengertian Dan Metode Penyelesaian SPLDV | Metode Penyelesaian SPLDV merupakan salah satu cabang dari sistem persamaan linier .SPLDV merupakan kependekan dari Sistem Persamaan Linier Dua Variabel . Lalu apakah yang di maksed dengan SPLDV ? Dan bagaimanakah metode penyelesaiannya ? Apakah metode penyelesaiannya sama hal nya dengan metode penyelesaian sistem linier seperti yang telah kita pelajari pada pembahasan sebelumnya ? Untuk lebih jelas lagi maka mari kita pelajari bersama kembali bagaimana metode penyelesaian sistem persamaan Linier Dua Variabel .
Metode Penyelesaian Sistem Persamaan Linier Dua Variabel ( SPLDV )
Sebelum kita mempelajari lebih mendalam tentang bagaimana metode penyelesaian sistem persamaan linier dua variabel , maka langkah pertama kita harus memahami pengertian , ciri – ciri dan hal – hal yang berhubungan dengan sistem persamaan linier variabel .
SPLDV , adalah suatu sistem persamaan atau bentuk relasi sama dengan dalam bentuk aljabar yang memiliki dua variabel dan berpangkat satu dan apabila digambarkan dalam sebuah grafik maka akan membentuk garis lurus . Dan karena hal ini lah maka persamaan ini di sebut dengan persamaan linier .
Ciri – ciri SPLDV :
- Menggunakan relasi tanda sama dengan ( = )
- Memiliki dua variabel
- Kedua variabel tersebut memiliki derajat satu ( berpangkat satu )
Hal – hal yang berhubungan dengan SPLDV :
a. Suku
Suku yaitu bagian dari suatu bentuk aljabar yang terdiri dari variabel , koefisien dan konstanta . Dan setiap suku di pisahkan dengan tanda baca penjumlahan ataupun pengurangan .
Contoh :
6x – y + 4 , maka suku – suku dari persamaan tersebut adalah 6x , -y dan 4
b. Variabel
Variabel , yaitu peubah atau pengganti suatu bilangan yang biasanya dilambangkan dengan huruf seperti x dan y .
Contoh :
Mika memiliki 2 buah nanas dan 5 buah jeruk . Jika dituliskan dalam bentuk persamaan adalah
misal : nanas = x dan jeruk = y , maka persamannya adalah 2x + 5y
c. Koefisien
Koefisien , yaitu suatu bilangan yang menyatakan banyaknya suatu jumlah variabel yang sejenis . Koefisien disebut juga dengan bilangan yang ada di depan variabel , karena penulisan sebuah persamaan koefifien berada di depan variabel .
Contoh :
Mika memiliki 2 buah nanas dan 5 buah jeruk . Jika di tulis dalam bentuk persamaan adalah :
misal : nanas = x dan jeruk = y , maka persamannya adalah 2x + 5y . Dimana 2 dan 5 adalah koefisien . Dan 2 adalah koefisien x dan 5 adalah koefisien y .
d. Konstanta
Konstanta , yaitu bilangan yang tidak diikuti dengan variabel , maka nilainya tetap atau konstan untuk berapapun nilai peubahnya .
Contoh :
2x + 5y + 7 , dari persamaan tersebut konstanta adalah 7 , karena 7 nilainya tetap dan tidak terpengaruh dengan berapapun variabelnya .
Syarat Sistem Persamaan Linier Dua Variabel dapat memiliki satu penyelesaian , yaitu :
- Ada lebih dari satu atau ada dua persamaan linier dua variabel sejenis .
- Persamaan Linier Dua Variabel yang membentuk Sistem Persamaan Linier Dua Variabel , bukan Persamaan Linier Dua Variabel yang sama .
Metode Penyelesaian Sistem Persamaan Linier Dua Variabel
A. Metode Substitusi atau metode Mengganti
Metode substitusi , yaitu metode atau cara menyelesaikan SPLDV dengan mengganti salah satu peubah atau variabel.
Contoh Soal :
1. Tentukan Himpunan penyelesaian dari persamaan x + 3y = 15 dan 3x + 6y = 30 .
Penyelesaian :
Langkah pertama :
x + 3y = 15
<=> x = -3y + 15 . . . .( 1 )
3x + 6y = 30 . . . .(2)
Lalu , masukkan persamaan ( 1 ) ke dalam persamaan (2) , untuk mencari nilai y , maka :
3x + 6y = 30
<=> 3 ( -3y +15 ) + 6y = 30
<=> -9y + 45 + 6y = 30
<=> -3y = 30 – 45
<=> -3y = -15
<=> y = 5
Selanjutnya untuk mencari nilai x maka , gunakan salah satu persamaan boleh persamaan (1) atau ( 2 ) :
x + 3y = 15
<=>x + 3 ( 5 ) = 15
<=> x + 15 = 15
<=> x = 0
atau
3x + 6y = 30
<=> 3x + 6 ( 5 ) = 30
<=> 3x + 30 = 30
<=> 3x = 0
<=> x = 0
Jadi , HP = { 0 , 5 }
2. Tentukan Penyelesaian dari persamaan 3x+ 5y = 16 , dan 4x + y = 10 , jika x = a dan y = b . Maka tentukan nilai a dan b !
Penyelesaian :
3x + 5y = 16 . . . .(1)
4x + y = 10
<=> y = -4x + 10 . . .(2 )
Langkah pertama substitusikan persamaan (2) ke dalam persamaan (1) :
3x + 5y = 16
<=> 3x + 5 ( -4x + 10 ) = 16
<=> 3x – 20x + 50 = 16
<=> -17x = 16 – 50
<=> -17x = -34
<=> x = 2
Lalu , substitusikan nilai x ke dalam persamaan (1) atau (2) :
3x + 5y = 16
<=> 3(2) + 5y = 16
<=> 6 +5y = 16
<=> 5y = 16 – 6
<=> 5y = 10
<=> y = 2
atau
4x + y = 10
<=> 4(2) + y = 10
<=> 8 +y = 10
<=> y = 2
Jadi , kita ketahui nilai x = 2 dan nilai y = 2 . Dan Yang ditanyakan adaah nilai a dan b , dimana x = a dan y = b , maka :
x = a , maka x = 2 dan y = b maka b = 2 .
B. Metode Eliminasi atau metode menghilangkan
Metode eliminasi , adalah Metode atau cara untuk menyelesaikan sistem persamaan linier dua variabel dengan cara mengeliminasi atau menghilngkan salah satu peubah ( variabel ) dengan menyamakan koefisien dari persamaan tersebut .
Cara untuk menghilangkan salah satu peubahnya yaitu dengan cara perhatikan tandanya , apabila tandanya sama [(+) dengan (+) atau (-) dengan (-) ] , maka untuk mengeliminasinya dengan cara mengurangkan . Dan sebaliknya apabila tandanya berbeda maka gunakanlah sistem penjumlahan .
Untuk lebih jelasnya , perhatikan contoh soal di bawah ini :
1. Tentukan Himpunan penyelesaian dari persamaan x + 3y = 15 dan 3x + 6y = 30 .
Penyelesaian :
Langkah pertama yaitu , menentukan variabel mana yang akan di eliminasi terlebih dahulu . Kali ini kita akan menghilangkan x terlebih dahulu , dan supaya kita temukan nilai y . Caranya yaitu :
3x + 6y = 30 : 3
<=> x + 2y = 10 . . . . ( 1 )
x + 3y = 15 . . . .(2)
Dari persamaan (1) dan (2) , mari kita eliminasi , sehingga hasilnya :
x + 3y = 15
x + 2y = 10 _
<=> y = 5
Selanjutnya , untuk mengetahui nilai x , maka caranya sebagai berikut :
x + 3y = 15 | x2 | <=> 2x + 6y = 30 . . . .( 3 )
3x + 6y = 30 | x1 | <=> 3x + 6y = 30 . . .. (4 )
Eliminasi antara persamaan (3) dengan (4 ) , yang hasilnya menjadi :
3x + 6y = 30
2x + 6y = 30 _
<=> x = 0
Maka , Himpunan penyelesaiannya adalah :
HP = { 0 . 5 }
2. Tentukan Penyelesaian dari persamaan 3x+ 5y = 16 , dan 4x + y = 10 , jika x = a dan y = b . Maka tentukan nilai a dan b !
Penyelesaian :
Langkah yang pertama , yaitu tentukan variabel mana yang akan di eliminasi terlebih dahulu perhatikan penyelesaian di bawah ini
3x+ 5y = 16 | x1 | <=> 3x + 5y = 16 . . . .( 1 )
4x + y = 10 | x5 | <=> 20x + 5y = 50 . . . ( 2 )
Dari persamaan (1 ) dan (2 ) , dapat kita eliminasi dan menghasilkan :
20x + 5y = 50
3x + 5y = 16 _
<=> 17 x + 0 = 34
<=. > x = 34 / 17
<=> x = 2
Selanjutnya , lakukan langkah yang sama namun kali ini yang harus sama x nya , maka caranya adalah :
3x+ 5y = 16 | x4 | <= > 12 x + 20y = 64 . . .(3)
4x + y = 10 | x3 | <=> 12x + 3y = 30 . . . .(4)
Persamaan (30 dan (4 ) , mari kita eliminasi untuk menghasilkan nilai y :
12 x + 20y = 64
12x + 3y = 30 _
<=> 0 + 17y = 34
<=> y = 2
Jadi , HP ={ 2 ,2 } , dan nilai a dan b adalah :
a= x = 2 dan b = y = 2
C. Metode Campuran ( eliminasi dan substitusi )
Metode campuran , yaitu suatu cara atau metode untuk menyelesaikan suatu persamaan linier dengan menguunakan dua metode yaitu metode eliminasi dan substitusi secara bersamaan . Untuk lebih jelasnya , perhatikan contoh di bawah ini :
Diketahui persamaan x + 3y = 15 dan 3x + 6y = 30 , dengan menggunakan metode campuran tentukanlah Himpunan penyelesaiannya !
Penyelesaian :
x + 3y = 15 | x3| <=> 3x +9x = 45
3x + 6y = 30 | 1 | <=> 3x + 6y = 30 _
0 + 3y = 15
y = 5
x + 3y = 15
<=> x + 3.5 = 15
<=> x + 15 = 15
<=> x = 0
Jadi , HP ={ 0 , 5 }
Demikian penjelasan mengenai Metode penyelesaian SPLDV . Mudah bukan ? prinsipnya sama dengan cara menyelesaikan persamaan linier . Dan yang perlu difahami benar yaitu bentuk sisitem persamaan linier dua variabel itu seperti apa . Kata kuncinya adalah dua variabel , berarti peubahnya ada dua yaitu x dan y atau simbol yang lainnya .
Dan diantara cara ketiga di atas , cara nomer tigalah yang paling efektif dan efisien . Kenapa demikian ? karena juka kita sedang menyelesaikan Soal UAS , pasti menjadi mempercepat waktu dan yang penting hasilnyapun benar .
Semoga dengan penjelasan di atas sedikit banyak dapat membantu menyelesaikan persoalan sistem persamaan linier dua variabel .
Memahami Sistem Persamaan Linier Dan Metode Penyelesaiannya
Sistem Persamaan Linier | Persamaan linier sama halnya dengan persamaan aljabar , yaitu merupakan sebuah sisitem hitung dalam ilmu matematika dan dapat digambarkan dalam bentuk garis lurus dalam sebuah grafik . Sistem persamaan linier disebut juga dengan sisitem persamaan garis . Dan pada pembahasan sebelumnya , telah kita pelajari rumus sistem persamaan garis lurus , jadi pasti kita masih ingat dong bagaimana gambaran tentang bentuk persamaan .
Lalu bagaimanakah cara atau metode dalam menyelesaikan sistem persamaan linier ? Pada pembahasan kali ini , kita akan mempelajari apa itu persamaan linier dan bagaimana metode dalam meyelesaikan persamaan linier secara lengkap dan tepat .
Sistem Persamaan Linier
Sebelum kita mempelajari bagaimana metode dalam menyelesaikan siste persamaan linier , maka kita harus memahami terlebih dahulu mengenai definisi kalimat terbuka dan definisi persamaan serta tentang sistem persamaan linier . Sehingga dalam menyelesaikan persamaan linier kita tidak bingung.
A. Pengertian Kalimat terbuka , persamaan dan persamaan linier
Kalimat Terbuka , yaitu suatu kalimat yang memiliki atau memuat variabel .
Persamaan , yaitu kalimat terbuka yang menyatakan hubugan sama dengan ( = ) .
Persamaan Linier , yaitu suatu persamaan yang setiap sukunya mengandung konstanta dengan variabelnya berderajat satu ( tunggal ) dan persamaan ini , dapat digambarkan dalam sebuah grafik dalam sistem koordinat kartesius .
Suatu Persamaan akan tetap bernilai benar atau EKWIVALENT ( < = > ) , Apabila ruas kiri dan ruas kanan ditambah atau dikurangi dengan bilangan yang sama .
Bentuk umum persamaan linier :
y = mx + b
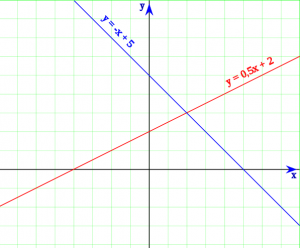
Contoh bentuk persamaan linier :
y = -x + 5
y = -05x + 2
Contoh bentuk grafik persamaan linier :
Dari gambar di atas , dapat kita simpulkan bahwasannya m atau gradiennya = 0,5 dan b atau titik potong sumbu y = 2 ( pada garis merah )
B. Metode Penyelesaian Persamaan Linier
Ada beberapa metode yang dapat digunakan dalam menyelesaikan sebuah permasalahan persamaan linier , metode – metode tersebut adalah :
a. Metode Substitusi
b. Metode Eliminasi
c. Metode Campuran ( eliminasi dan substitusi )
d. Metode grafik
Berikut adalah penjelasan lebih rinci mengenai metode penyelesaian persamaan linier :
- Metode Substitusi
Metode subsitusi yaitu metode atau cara menyelesaikan persamaan linier dengan mengganti salah satu peubah dari suatu persamaan dengan peubah yang diperoleh dari persamaan linier yang lainnya .
Untuk lebih jelasnya lagi , perhatikan contoh berikut ini :
Diketahui persamaan x + 3y = 7 dan 2x + 2y = 6 , tentukan Himpunana Penyelesaiannya :
Penyelesaiannya :
x + 3y = 7
< = > x = -3y + 7 . . . .( 1 )
Lalu , masukkan persamaan ( 1 ) ke dalam persamaan ( 2 ) untuk mencari nilai y
2x + 2y = 6
< = > 2 ( -3y + 7 ) + 2y = 6
< = > -6y + 14 + 2y = 6
< = > -6y + 2y = 6 – 14
< = > -4y = – 8
< = > y = 2
Gunakan persamaan antara persamaan ( 1 ) atau ( 2 ) untuk mencari nilai x
x + 3y = 7
< = > x + 3 ( 2 ) = 7
< = > x + 6 = 7
< = > x = 1
Jadi , HP = { 1 , 2 }
2. Meode Eliminasi
Metode Eliminasi , yaitu metode penyelesaian sistem persamaan linir dengan cara mengeliminasi atau menghilangkan salah satu peubah dengan menambahkan atau mengurangkan dengan menyamakan koefisien yang akan dihilangkan tanpa memperhatikan nilai positif atau negatif .
Apabila peubah yang akan dihilangkan bertanda sama , maka untuk mengeliminasi menggunakan sistem operasi pengurangan . Dan sebaliknya apabila peubah yang akan dihilangkan bertanda berbeda , maka untuk mengaliminasi menggunakan operasi penjumlahan .
Utuk lebih jelasnya , perhatikan contoh berikut ini :
Masih dengan contoh yang sama , namun dengan cara yang berbeda yaitu :
Diketahui dua persamaan x + 3y = 7 dan 2x + 2y = 6 , tentukan HP dari persamaan tersebut !
Langkah pertama adalah lakukan eliminasi dengan mengurangkan untuk menghilangkan peubah atau koefisien x untuk mengetahui nilai y
2x + 2y = 6 : 2
< = > x + y = 3
lalu , lakukan
x + 3y = 7
x + y = 3 _
2y = 4
y = 2
Langkah selanjutnya adalah lakukan eliminasi dengan mengurangkan untuk menghilangkan peubah atau koefisien y untuk mengetahui nilai x
2x + 2y = 6 | x3 | < = > 6x + 6y = 18
x + 3y = 7 | x 2 | < = > 2x + 6 y = 14 _
4x + 0 = 4
x = 1
Jadi , Himpunan penyelesaian yang dihasilkan sama yaitu HP = { 1 , 2 }
3. Metode Campuran ( antara eliminasi dan substitusi )
Yang dimaksud dari metode ini , yaitu kita dalam mencari himpunan penyelesaian menggunakan dua metode boleh gunakan eliminasi terlebih dahulu setelah diketahui salah satu nilai peubah baik itu x atau y maka selanjutnya masukkan ke dalam metode substitusi atau sebaliknya .
Untuk lebih jelasnya , perhatikan contoh berikut :
Diketahui dua persamaan x + 3y = 7 dan 2x + 2y = 6 , tentukan HP dari persamaan tersebut !
Langkah pertama lakukan metode eliminasi , untuk mecari nilai x
2x + 2y = 6 | x3 | < = > 6x + 6y = 18
x + 3y = 7 | x 2 | < = > 2x + 6 y = 14 _
4x + 0 = 4
x = 1
Selanjutnya substitusikan nilai x ke dalam salah satu persamaan :
x + 3y = 7
< = > 1 + 3y = 7
< = > 3y = 7 – 1
< = > 3y = 6
< = > y = 2
Maka hasilnyapun sama yaitu HP = { 1 , 2 }
4. Metode Grafik
Metode grafik , yaitu dengan menggambarkan dua persamaan pada grafik kartesius , dan himpunan penyelesaiannya dihasilkan dari titik potong dari kedua garis tersebut . Yang perlu diperhatikan yaitu ketika menggambar titik sumbu kartesiusnya harus sama dan konsisten .
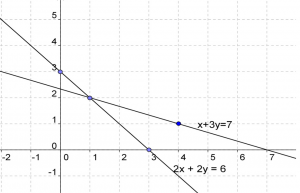
Untuk lebih jelasnya perhatikan gambar grafik berikut :
Gambarlah grafik persamaan x + 3y = 7 dan 2x + 2y = 6 , dan tentukan titik potongnya
Dari gambar di atas , maka kita dapat melihat bahwa titik potongnya berada pada titik { 1 , 2 } dan dengan kata lain HP = { 1 , 2 }
Demikian penjelasan mengenai sistem persamaan linier dan metode penyelesaiannya . Semoga dengan penjelasan diatas kita dapat lebih faham mengenai apa itu sistem persamaan dan cara – cara dalam menyelesaikannya . Untuk memudahkan dalam menyelesaikan sistem persamaan , langkah yang pertama yaitu memahami bentuk dari persamaan linier itu sendiri dan selanjutnya kita fahami cara – caranya . Semoga bermanfaat dan dapat membantu permasalahan dalam menyelesaikan persamaan linier .


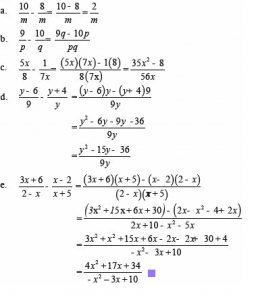
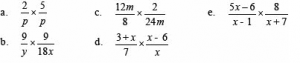

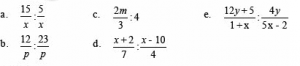

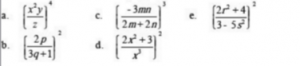



0 Response to "√Operasi Hitung Pecahan Aljabar Dan Contoh Soalnya Lengkap Kuncinya"
Posting Komentar