Bentuk umum dari pecahan yaitu a/b dibaca a per b dengan a dan b merupakan bilangan bulat serta b tidak sama dengan nol ( 0 ).
pecahan a/b
a disebut dengan pembilang
b disebut dengan penyebut.
Jika pembilang dan penyebut suatu pecahan dikali ataupun dibagi dengan bilangan yang sama besar maka akan didapat pecahan yang senilai.
misal :
1/2 dikali dengan 2/2 maka hasilnya 2/4, nilai 1/2 = 2/4. meski bilangan pembilang dan penyebutnya berbeda akan tetapi nilainya tetap sama. Ingat invers dari perkalian ? ya benar berapapun bilangannya jika dikalikan dengan satu maka hasilnya adalah bilangan itu sendiri.
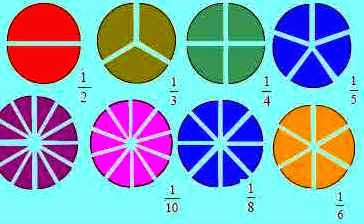
artinya 2/2 itu hasilnya 1 jadi 1/2 dikalikan dengan 1 ya hasilnya tetep setengah. oke ? mudah bukan.
mengubah bentuk pecahan biasa kedesimal dapat dilakukan dengan membagikan pembilang dengan penyebutnya. jika penyebutnya 10, 100, 1000, 10000, ... , maka banyaknya koma pada pecahan desimal sesuai dengan penyebutnya, artinya jika penyebutnya 10 maka hanya ada 1 angka dibelakang koma, jika 100 maka 2 angka dibelakang koma begitu seterusnya.
contoh :
1/10 = 0,1
1/100 = 0,01
1/1000 = 0,001
12/10000 = 0,0012
2/5 = ...
jadikan penyebutnya menjadi sepuluh dengan mengalikan 2 INGAT jika penyebutnya dikalikan dengan 2 maka begitu juga dengan pembilangnya.
2/5 x 2/2 = 4/10 maka bentuk desimal dari 2/5 adalah 0,4.
Mengubah pecahan desimal ke bentuk pecahan biasa
Dalam mengubah pecahan desimal ke pecahan biasa kita harus memperhatika berapa angka dibelakang koma dari pecahan desimal tersebut. INGAT !! jika ada 1 angka dibelakang koma berarti penyebutnya 10. seperti yang sudah dijelaskan diatas.
Untuk lebih mudahnya perhatika contoh berikut :
0,2 = 2/10 disederhanakan menjadi 1/5
0,25 = 25/100 disederhanakan menjadi 1/4
2,65 = 2 + 65/100 disederhanakan menjadi 2 13/20
mudah bukan. -_-
Mengubah pecahan biasa ke bentuk persen
untuk mengubah pecahan biasa menjadi persen yang wajib dilakukan adalah mengubah penyebut dari pecahan tersebut menjadi berpenyebut 100 atau mengalikan pecahan biasa tersebut dengan 100%
contoh :
1/4 = 1/4 x 25/25 ( kenapa dikalikan 25/25 ? ya benar untuk memperoleh penyebut 100 )
1/4 x 25/25 = 25/100 = 25%
oia tidak selalu pembilang dan penyebutnya dikalikan dengan bilangan 25 lho ya pengalian disesuaikan dengan penyebut dari pecahan biaa.
contoh lain 3/8
3/8 x 100% = 300/8 % = 37,5%
Admin cukupkan materi bilangan pecahan kali ini soalnya udah ngantuk dan mau makan sahur dulu ya udah laper berat nih soalnya :D. Kuadrat dan akar kuadrat tampak asing ditelinga ketika dulu baru pertama kali mendengar kosakata baru ini, ya akar kuadrat kali ini admin akan membahas pengertian akar kuadrat disertai dengan contoh pembahasannya.
untuk sembarang bilangan bulat b maka :
b2 = b x b
kuadrat juga biasa disebut dengan pangkat 2.
Nilai √a = b jika b2 = a, dengan b merupakan bilangan positif atau nol.
Misal : √49 = 7, jawaban ini benar karena 72 = 49
Gimana sudah pahamkan cara menghitung akar kuadratnya ? pastinya sudah lah...
Demikian artikel sederhana mengenai kuadrat dan akar kuadrat yang bisa admin sajikan dan berikut tabel kuadrat dan akar kuadrat.
12 = 1
22 = 4
32 = 9
42 = 16
52 = 25
62 = 36
72 = 49
82 = 64
92 = 81
102 = 100
112 = 121
122 = 144
132 = 169
142 = 196
152 = 225
162 = 256
172 = 289
182 = 324
192 = 361
202 = 400
212 = 441
222 = 484
232 = 529
242 = 576
252 = 625
262 = 676
272 = 729
282 = 784
292 = 841
302 = 900
312 = 961
322 = 1024
332 = 1089
342 = 1156
352 = 1225
362 = 1296
372 = 1369
382 = 1444
392 = 1521
402 = 1600
412 = 1681
422 = 1764
432 = 1849
442 = 1936
452 = 2025
462 = 2116
472 = 2209
482 = 2304
492 = 2401
502 = 2500
512 = 2601
522 = 2704
532 = 2809
542 = 2916
552 = 3025
562 = 3136
572 = 3249
582 = 3364
592 = 3481
602 = 3600
612 = 3721
622 = 3844
632 = 3969
642 = 4096
652 = 4225
662 = 4356
672 = 4489
682 = 4624
692 = 4761
702 = 4900
712 = 5041
722 = 5184
732 = 5329
742 = 5476
752 = 5625
762 = 5776
772 = 5929
782 = 6084
792 = 6241
802 = 6400
812 = 6561
822 = 6724
832 = 6889
842 = 7056
852 = 7225
862 = 7396
872 = 7569
882 = 7744
892 = 7921
902 = 8100
912 = 8281
922 = 8464
932 = 8649
942 = 8836
952 = 9025
962 = 9216
972 = 9409
982 = 9604
992 = 9801
1002 = 10000
Untuk tabel akar kuadrat tinggal dibalik misal : √9801 = 99 . oke ? bisa dipahami kan ?
selamat belajar dan terus semangat. salam matika
Materi Bilangan Bulat untuk tingkat SMP, kali ini admin akan share mengenai apa itu bilangan bulat setelah beberapa minggu ini tidak pernah posting akhirnya keluar lagi semangat untuk memberikan asupan materi pada blog ini.
 Sebelum membahas lebih lanjut mari kita kaji dulu pengertian bilangan bulat, matematika tidak akan lepas dari yang namanya bilangan oleh karena itu menguasai materi bilangan bulat juga termasuk penting kadang kita sering lupa apa saja sih himpunan dari bilangan bulat itu sendiri.
Sebelum membahas lebih lanjut mari kita kaji dulu pengertian bilangan bulat, matematika tidak akan lepas dari yang namanya bilangan oleh karena itu menguasai materi bilangan bulat juga termasuk penting kadang kita sering lupa apa saja sih himpunan dari bilangan bulat itu sendiri.
Jadi secara ringkas bilangan bulat terdiri dari bilangan bulat negatif, bilangan bulat negatif dan nol. Lambang bilangan bulat disimbolkan dengan huruf Z (seperti gambar diatas ) yang berasal dari kata Zahlen (dari bahasa Jerman yang artinya "bilangan").
Dalam gambar garis bilangan diatas bilangan 2 terletak di sebelah kanan bilangan -1 maka 2 lebih besar dari -1 bisa ditulis 2 > -1, -4 terletak disebelah kiri -2 maka -4 lebih kecil dari -1 ( -4 < -1 ) jadi dapat disimpulkan bahwa nilai bilangan semakin kekeri maka bilangan itu semakin kecil dan sebaliknya jika semakin kekanan maka bilangan itu semakin besar.
Contoh soal bilangan bulat Sisipkanlah lambang < atau > diantara pasangan bilangan berikut agar menjadi kalimat yang benar !
a. 7, ... -7
b. 10, ... ,-11
c. -45, ... , -20
d. -14, ... , 14
e. 56, ... ,-65
Penjumlahan dan sifatnya
Untuk mempermudah dalam memahami penjumlahan bilangan bulat kita dapat menggunakan bantuan garis bilangan, seperti contoh dibawah ini :
Tentukan hasil -4 + 3.
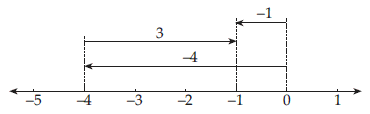
pertama tarik garis kekiri ( kenapa kekiri ? kan bilangannya negatif ) dari nol sampai -4 kemudian tarik garis kekanan sepanjang 3 skala, nah dapet deh jawabannya -1. mudah kan ?
Sifat komutatif penjumlahan
a + b = b + a, misal apa bila ada soal 6 + 3 itu sama dengan 3 + 6.
Sifat asosiatif penjumlahan
( a + b ) + c = a + ( b + c ), artinya kalian bisa menjumlahkan a dan b lebih dulu kemudian baru ditambah dengan c, atau b dan c dijumlahkan lebih dulu baru dijumlahkan dengan a.
Sampai disini dulu materi bilangan bulat nya dan materi ini dilanjutkan ke operasi bilangan bulat
pecahan a/b
a disebut dengan pembilang
b disebut dengan penyebut.
Jika pembilang dan penyebut suatu pecahan dikali ataupun dibagi dengan bilangan yang sama besar maka akan didapat pecahan yang senilai.
misal :
1/2 dikali dengan 2/2 maka hasilnya 2/4, nilai 1/2 = 2/4. meski bilangan pembilang dan penyebutnya berbeda akan tetapi nilainya tetap sama. Ingat invers dari perkalian ? ya benar berapapun bilangannya jika dikalikan dengan satu maka hasilnya adalah bilangan itu sendiri.

artinya 2/2 itu hasilnya 1 jadi 1/2 dikalikan dengan 1 ya hasilnya tetep setengah. oke ? mudah bukan.
Mengubah pecahan
Mengubah pecahan biasa kedalam bentuk pecahan desimal.mengubah bentuk pecahan biasa kedesimal dapat dilakukan dengan membagikan pembilang dengan penyebutnya. jika penyebutnya 10, 100, 1000, 10000, ... , maka banyaknya koma pada pecahan desimal sesuai dengan penyebutnya, artinya jika penyebutnya 10 maka hanya ada 1 angka dibelakang koma, jika 100 maka 2 angka dibelakang koma begitu seterusnya.
contoh :
1/10 = 0,1
1/100 = 0,01
1/1000 = 0,001
12/10000 = 0,0012
2/5 = ...
jadikan penyebutnya menjadi sepuluh dengan mengalikan 2 INGAT jika penyebutnya dikalikan dengan 2 maka begitu juga dengan pembilangnya.
2/5 x 2/2 = 4/10 maka bentuk desimal dari 2/5 adalah 0,4.
Mengubah pecahan desimal ke bentuk pecahan biasa
Dalam mengubah pecahan desimal ke pecahan biasa kita harus memperhatika berapa angka dibelakang koma dari pecahan desimal tersebut. INGAT !! jika ada 1 angka dibelakang koma berarti penyebutnya 10. seperti yang sudah dijelaskan diatas.
Untuk lebih mudahnya perhatika contoh berikut :
0,2 = 2/10 disederhanakan menjadi 1/5
0,25 = 25/100 disederhanakan menjadi 1/4
2,65 = 2 + 65/100 disederhanakan menjadi 2 13/20
mudah bukan. -_-
Mengubah pecahan biasa ke bentuk persen
untuk mengubah pecahan biasa menjadi persen yang wajib dilakukan adalah mengubah penyebut dari pecahan tersebut menjadi berpenyebut 100 atau mengalikan pecahan biasa tersebut dengan 100%
contoh :
1/4 = 1/4 x 25/25 ( kenapa dikalikan 25/25 ? ya benar untuk memperoleh penyebut 100 )
1/4 x 25/25 = 25/100 = 25%
oia tidak selalu pembilang dan penyebutnya dikalikan dengan bilangan 25 lho ya pengalian disesuaikan dengan penyebut dari pecahan biaa.
contoh lain 3/8
3/8 x 100% = 300/8 % = 37,5%
Admin cukupkan materi bilangan pecahan kali ini soalnya udah ngantuk dan mau makan sahur dulu ya udah laper berat nih soalnya :D. Kuadrat dan akar kuadrat tampak asing ditelinga ketika dulu baru pertama kali mendengar kosakata baru ini, ya akar kuadrat kali ini admin akan membahas pengertian akar kuadrat disertai dengan contoh pembahasannya.
Pengertian Kuadrat
Kuadrat suatu belangan adalah perkalian suatu bilangan dengan bilangan itu sendiri.untuk sembarang bilangan bulat b maka :
b2 = b x b
kuadrat juga biasa disebut dengan pangkat 2.
Pengertian Akar Kuadrat
√a adalah bilangan positif atau nol yang jika dikuadratkan menghasilkan a. Paham ? untuk lebih jelasnya silahkan perhatikan contoh berikut.Nilai √a = b jika b2 = a, dengan b merupakan bilangan positif atau nol.
Misal : √49 = 7, jawaban ini benar karena 72 = 49
Gimana sudah pahamkan cara menghitung akar kuadratnya ? pastinya sudah lah...
Demikian artikel sederhana mengenai kuadrat dan akar kuadrat yang bisa admin sajikan dan berikut tabel kuadrat dan akar kuadrat.
12 = 1
22 = 4
32 = 9
42 = 16
52 = 25
62 = 36
72 = 49
82 = 64
92 = 81
102 = 100
112 = 121
122 = 144
132 = 169
142 = 196
152 = 225
162 = 256
172 = 289
182 = 324
192 = 361
202 = 400
212 = 441
222 = 484
232 = 529
242 = 576
252 = 625
262 = 676
272 = 729
282 = 784
292 = 841
302 = 900
312 = 961
322 = 1024
332 = 1089
342 = 1156
352 = 1225
362 = 1296
372 = 1369
382 = 1444
392 = 1521
402 = 1600
412 = 1681
422 = 1764
432 = 1849
442 = 1936
452 = 2025
462 = 2116
472 = 2209
482 = 2304
492 = 2401
502 = 2500
512 = 2601
522 = 2704
532 = 2809
542 = 2916
552 = 3025
562 = 3136
572 = 3249
582 = 3364
592 = 3481
602 = 3600
612 = 3721
622 = 3844
632 = 3969
642 = 4096
652 = 4225
662 = 4356
672 = 4489
682 = 4624
692 = 4761
702 = 4900
712 = 5041
722 = 5184
732 = 5329
742 = 5476
752 = 5625
762 = 5776
772 = 5929
782 = 6084
792 = 6241
802 = 6400
812 = 6561
822 = 6724
832 = 6889
842 = 7056
852 = 7225
862 = 7396
872 = 7569
882 = 7744
892 = 7921
902 = 8100
912 = 8281
922 = 8464
932 = 8649
942 = 8836
952 = 9025
962 = 9216
972 = 9409
982 = 9604
992 = 9801
1002 = 10000
Untuk tabel akar kuadrat tinggal dibalik misal : √9801 = 99 . oke ? bisa dipahami kan ?
selamat belajar dan terus semangat. salam matika
Materi Bilangan Bulat untuk tingkat SMP, kali ini admin akan share mengenai apa itu bilangan bulat setelah beberapa minggu ini tidak pernah posting akhirnya keluar lagi semangat untuk memberikan asupan materi pada blog ini.
 Sebelum membahas lebih lanjut mari kita kaji dulu pengertian bilangan bulat, matematika tidak akan lepas dari yang namanya bilangan oleh karena itu menguasai materi bilangan bulat juga termasuk penting kadang kita sering lupa apa saja sih himpunan dari bilangan bulat itu sendiri.
Sebelum membahas lebih lanjut mari kita kaji dulu pengertian bilangan bulat, matematika tidak akan lepas dari yang namanya bilangan oleh karena itu menguasai materi bilangan bulat juga termasuk penting kadang kita sering lupa apa saja sih himpunan dari bilangan bulat itu sendiri.Pengertian Bilangan Bulat
Bilangan bulat adalah sekumpulan bilangan yang anggotanya terdiri dari bilangan negatif dan bilangan cacah. dari pengertian tersebut dapat kita simpulkan bahwa bilangan bulat merupakan semua bilangan baik itu negatif atau positif termasuk juga nol. Tapi ingat pecahan tidak termasuk dalam bilangan bulat.Jadi secara ringkas bilangan bulat terdiri dari bilangan bulat negatif, bilangan bulat negatif dan nol. Lambang bilangan bulat disimbolkan dengan huruf Z (seperti gambar diatas ) yang berasal dari kata Zahlen (dari bahasa Jerman yang artinya "bilangan").
Bilangan bulat dalam garis bilangan
Didalam garis bilangan bilangan bulat dapat dinyatakan seperti pada gambar dibawah :Contoh soal bilangan bulat Sisipkanlah lambang < atau > diantara pasangan bilangan berikut agar menjadi kalimat yang benar !
a. 7, ... -7
b. 10, ... ,-11
c. -45, ... , -20
d. -14, ... , 14
e. 56, ... ,-65
Operasi Hitung Bilangan Bulat
Setelah memahami pengertian bilangan bulat diatas selanjutnya kita akan membahas mengenai bagaimana operasi bilangan bulat tambah, kurang, kali dan bagi serta sifat-sifat yang terkandung dalam operasi bilangan tersebut.Penjumlahan dan sifatnya
Untuk mempermudah dalam memahami penjumlahan bilangan bulat kita dapat menggunakan bantuan garis bilangan, seperti contoh dibawah ini :
Tentukan hasil -4 + 3.

pertama tarik garis kekiri ( kenapa kekiri ? kan bilangannya negatif ) dari nol sampai -4 kemudian tarik garis kekanan sepanjang 3 skala, nah dapet deh jawabannya -1. mudah kan ?
Sifat komutatif penjumlahan
a + b = b + a, misal apa bila ada soal 6 + 3 itu sama dengan 3 + 6.
Sifat asosiatif penjumlahan
( a + b ) + c = a + ( b + c ), artinya kalian bisa menjumlahkan a dan b lebih dulu kemudian baru ditambah dengan c, atau b dan c dijumlahkan lebih dulu baru dijumlahkan dengan a.
Sampai disini dulu materi bilangan bulat nya dan materi ini dilanjutkan ke operasi bilangan bulat

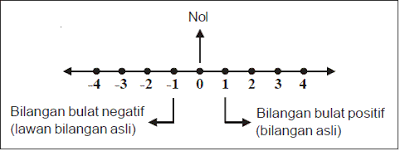 Bilangan negatif selalu digambarkan disebelah kiri
Bilangan negatif selalu digambarkan disebelah kiri
0 Response to "√Materi Bilangan Pecahan Biasa, Desimal, Persen Lengkap Kuncinya"
Posting Komentar