Rumus Persamaan Kuadrat Matematika Lengkap
Rumus Persamaan Kuadrat – Pengertian Persamaan Kuadrat menurut para ahli Matematika sering diartikan sebagai kalimat terbuka yg menyatakan hubungan sama dg (=) dan pangkat tertinggi dari variabelnya yg bernilai dua. Persamaan Kuadrat Matematika ini mempunyai bentuk umum seperti y = ax² + bx + c. Adapun untuk Rumus Menghitung Persamaan Kuadrat sering disamakan untuk menentukan Akar – Akar Persamaan Kuadrat dan Rumus Mencari Persamaan Kuadrat ini sering muncul didalam Ujian Sekolah maupun Ujian Nasional ditingkat Sekolah Menengah Atas (SMA) sehingga pembahasan tentang Persamaan Kuadrat ini sangatlah penting sekali bagi Siswa Siswi tingkat SMA.
Lalu sekali lagi Bentuk Umum Persamaan Kuadrat y = ax² + bx + c dengan a ≠ 0 dan penjelasan tentang huruf a, b dan c didalam Bentuk Umum Persamaan Kuadrad diatas disebut dengan Koefisien yang terbagi menjadi Koefisien Kuadrat a ialah Koefisien dari x², Koefisien Linier b ialah Koefisien dari x dan Koefisien c ialah Koefisien Konstan atau disebut juga dengan Suku Bebas. Sebagai tambahan saja bahwa Rumus Persamaan Kuadrat dengan Rumus Akar Persamaan Kuadrat itu sama sehingga kalian harus benar – benar mengetahui dan pahami dengan seksama artian tentang huruf a, b dan c didalam Rumus Persamaan Kuadrad tersebut.
Rumus Persamaan Kuadrat dan Akar – Akar Persamaan Kuadrat
Kemudian didalam Mencari dan Menghitung Nilai Akar Persamaan Kuadrat sendiri bisa menggunakan Tiga cara yang pertama ialah dengan cara Memfaktorkan atau Faktorisasi atau Pemfaktoran, Cara Mencari Akar Persamaan Kuadrat yang kedua ialah melengkapkan dengan Kuadrat Sempurna dan Cara Menghitung Akar Persamaan Kuadrat yang ketiga ialah dengan menggunakan Rumus.
Memfaktorkan dan Mencari Faktor Persamaan Kuadrat
Pengertian tentang Faktorisasi Akar Persamaan Kuadrat atau Pemfaktoran Persamaan Kuadrat ialah menyatakan penjumlahan suku – suku bentuk Aljabar yang dijadikan bentuk perkalian Faktor – Faktor. Sedangkan untuk Memfaktorkan Akar Persamaan Kuadrat ialah membuat persamaan kuadrat tersebut menjadi perkalian 2 (Dua) persamaan Linear.
Cara Melengkapkan Kuadrat Sempurna
Teknik Melengkapkan Kuadrat Sempurna ialah Teknik untuk memperoleh bentuk Kuadrat dari sebuah bilangan sehingga langkah terakhir dari teknik kuadrat sempurna ialah dengan mendapatkan bentuk.
(x – a)² = p
Dibawah ini contoh tentang Akar Persamaan Kuadrat dengan cara dan teknik Melengkapkan Kuadrat Sempurna.
Rumus Kuadratis atau Rumus ABC
Rumus Kuadratis atau dikenal dengan nama Rumus ABC dapat dipakai untuk menghitung Nilai Akar – Akar Persamaan Kuadrat yang tergantung dari Nilai – Nilai a, b dan c didalam Koefisien Persamaan Kuadrat dan Rumus Persamaan Kuadrat menggunakan Rumus ABC ini bisa dilihat dibawah ini.
Contoh Soal Persamaan Kuadrat dan Jawabannya
Mungkin hanya seperti itu saja penjelasan dan ulasan lengkap tentang Rumus Persamaan Kuadrat Matematika dan semoga saja apa yang sudah saya tulis diatas dapat bermanfaat untuk kalian semua sebagai seorang Siswa Siswi tingkat Sekolah Menengah Atas (SMA) karena sekali lagi ilmu Matematika tentang Persamaan Kuadrat sangatlah penting sama halnya tentang Rumus Trigonometri Matematika dan sering muncul di Soal – Soal Ujian baik Ujian Akhir Sekolah maupun Ujian Nasional sehingga kalian benar – benar harus jeli dan memahami tentang kedua Ilmu Matematika tersebut agar bisa mengerjakan Soal – Soal dengan benar.
Rumus Cosinus Trigonometri Matematika Lengkap
Rumus Cosinus Trigonometri – Sebelum membahas secara lebih dalam tentang Cara Menghitung Cosinus Trigonometri Matematika, ada baiknya bagi kalian sebagai pelajar untuk mengetahui arti dari Cosinus Trigonometri itu sendiri karena Pengertian Cosinus Trigonometri didalam Matematika ialah perbandingan sisi Segitiga yg terletak di Sudut dg Sisi Miring dan Segitiga tersebut ialah Segitiga Siku – Siku atau Sudut Segitiga 90 Derajat. Adapun untuk Pengertian Trigonometri Matematika itu sendiri mempunyai pengertian salah satu Cabang ilmu Matematika yg berhadapan dengan Sudut Segitiga dan Cosinus sendiri merupakan salah satu Fungsi Trigonometri.
Karena didalam Fungsi Trigonometri Matematika mempunyai tiga macam yakni Sinus (sin), Cosinus (cos) dan Tangen (tan). Oleh karena itu kalian sebagai seorang Pelajar atau Siswa dan Siswi harus mengenal lebih jauh tentang Fungsi Trigonometri sinus, cosinus dan tangen ini karena tidak bisa dipungkiri bahwa di tingkat Sekolah Menengah Atas (SMA) banyak sekali Soal – Soal Ujian baik itu didalam Ujian Sekolah ataupun didalam Ujian Nasional yang membahas atau mengulas untuk mencari nilai Trigonometri dengan menggunakan Rumus Trigonometri Matematika dan Rumus Mencari Sinus, Cosinus dan Tangen sehingga jika kalian sudah memahami tentang ilmu Trigonometri Matematika maka kalian akan dengan mudah mengerjakan Soal – Soal Trigonometri dan Geometri karena keduanya hampir sama.
Rumus Cosinus Trigonometri Matematika
Kalian bisa melihat Gambar Segitiga Siku – Siku atau Segitiga Sudut 90 Derajat diatas maka Nilai Cosinus mempunyai nilai perhitungan seperti ini, cos A = b/c dan cos B = a/c. Sedangkan untuk Cara Mencari Nilai Cosinus Positif bisa kalian temukan di Kuadran I dan IV (Kuadran I dan IV merupakan Tabel Sudut Istimewa Trigonometri) dan untuk Cara Menghitung Nilai Cosinus Negatif bisa kalian lihat di Kuadran II dan Kuadran III (Kuadran II dan Kuadran III merupakan Tabel Sudut Istimewa Trigonometri).
Rumus Menghitung Nilai Cosinus Trigonometri
Gambar diatas merupakan Rumus Cosinus Trigonometri Matematika dan untuk nilai cos 0 derajat, nilai cos 15 derajat, nilai cos 30 derajat, nilai 45 derajat, nilai 60 derajat, nilai 75 derajat dan nilai 90 derajat merupakan nilai cosinus di dlm Sudut Istimewa Trigonometri sehingga bagi kalian sebagai seorang pelajar memang harus mengenal dan memahami Nilai Sinus, Cosinus dan Tangen didalam Tabel Sudut Istimewa Trigonometri karena nilai sin, cos dan tan tidak akan luput dari tabel tersebut. Mungkin cukup sekian saja pembahasan tentang Pengertian Cosinus Trigonometri dan Rumus Menghitung Nilai Cosinus Trigonometri, semoga saja apa yang sudah saya tuliskan ini mampu memberikan manfaat untuk kalian sebagai pelajar baik pelajar tingkat SMP (Sekolah Menengah Pertama) dan SMA (Sekolah Menengah Atas).
Cara Menghitung Sinus Trigonometri Matematika
Cara Menghitung Sinus – Sebelum membahas tentang Cara Menghitung Nilai Sinus ada baiknya jika kalian mengetahui terlebih dahulu tentang Pengertian Sinus didalam Ilmu Matematika karena Sinus dalam Matematika ialah perbandingan Sisi dlm Segitiga yg ada didepan Sudut dg Sisi Miring-nya, hanya saja perlu kalian ingat bahwa Segitiga tersebut merupakan Segitiga Siku2 atau salah satu Sudut Segitiga itu memiliki nilai sebesar 90 Derajat. Adapun untuk Sinus sendiri didalam Matematika merupakan salah satu Fungsi Trigonometri karena didalam Trigonometri tersebut mempunyai beberapa Fungsi Trigonometri yang seperti Sinus (sin), Cosinus (cos) dan Tangen (tan).
Kemudian untuk Pengertian Trigonometri itu yaitu merupakan cabang dlm ilmu Matematika yang berhadapan dg sudut segitiga dan dasar dari Cabang Trigonometri tersebut ialah konsep kesebangunan segitiga siku – siku dan sisi – sisi yg bersesuaian pd 2 buah bangun datar yg sebangun dengan memiliki perbandingan yg sama dan mempunyai Sudut Istimewa Trigonometri, perlu kalian ketahui bahwa Cabang Trigonometri ini memiliki hubungan dengan Geometri karena banyak yang mengatakan bahwa Trinogometri termasuk bagian dari Geometri sehingga bagi kalian seorang Pelajar maupun Siswa yang sudah mengenal dan paham tentang Geometri maka tidak akan sulit dalam mempelajari Cabang Trigonometri dan Rumus Trigonometri Matematika yang ada.
Cara Menghitung Sinus Trigonometri Matematika
Kalian bisa melihat Gambar Segitiga 90 derajat diatas dan berdasarkan definisi atau gambar Segitiga 90 derajat diatas maka Nilai Sinus ialah sin A = a/c dan sin B = b/c. Lalu untuk Nilai Sinus Positif terdapat didalam Kuadran I dan II (Kuadran I dan II ialah Tabel Sudut Istimewa Trigonometri) dan untuk Nilai Sinus Negatif terdapat didlm Kuadran III dan IV (Kuadran III dan IV juga merupakan Tabel Sudut Istimewa Trigonometri), sedangkan untuk Hubungan Sinus dg Kosekan mempunyai nilai csc A = 1/ sin A.
Rumus Sinus Trigonometri Matematika
Diatas merupakan Cara Mencari Nilai Sinus Trigonometri dan nilai sin 0 derajat, sin 15 derajat, sin 30 derajat, sin 45 derajat, sin 60 derajat, sin 75 derajat dan sin 90 derajat merupakan Nilai Sinut dalam Sudut Istimewa Trigonometri sehingga jika kalian ingin menghitung nilai sin maka akan mudah jika melihat gambar diatas karena perlu kalian ketahui bahwa Rumus Trigonometri Matematika memang sedikit sulit untuk dipelajari, tetapi Trigonometri sering muncul di Soal – Soal Ujian Sekolah dan Ujian Nasional sehingga kalian sebagai seorang pelajar harus benar – benar mengerti dan memahami ilmu Trigonometri ini.



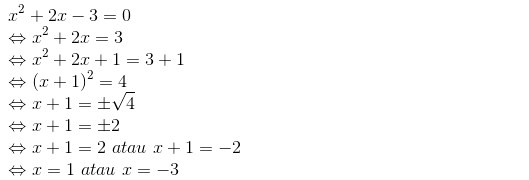

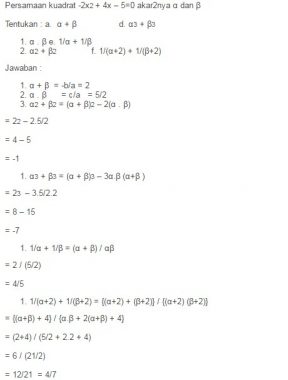
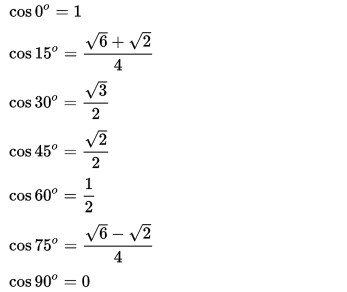

0 Response to "√Rumus Persamaan Kuadrat Matematika Lengkap Lengkap Kuncinya"
Posting Komentar